Inequality: In mathematics, an inequality is a statement that compares two values, expressions, or quantities using a relation symbol such as "greater than" (>), "less than" (<), "greater than or equal to" (≥), "less than or equal to" (≤), or "not equal to" (≠). An inequality indicates that the values or expressions being compared are not equal.
Combining like terms: In algebra, combining like terms refers to the process of simplifying an expression by adding or subtracting terms that have the same variable raised to the same power.
Inverse operations to isolate: In algebra, inverse operations are operations that undo each other. For example, addition and subtraction are inverse operations, as are multiplication and division. To isolate a variable in an equation or inequality, you can use inverse operations to undo the operations that are being performed on the variable.
To solve the inequality -13x + 46 > -45, you need to isolate the variable (x) on one side of the inequality.
1. First, you can subtract 46 from both sides of the inequality to get:
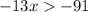
2. Then, divide both sides of the inequality by -13 (remember that when you divide or multiply by a negative number, you need to flip the inequality sign) to get:
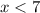
Therefore, the solution to the inequality is x < 7. To check, you can substitute any value less than 7 into the inequality to see if it's true. For example, if you plug in x = 5, you get:
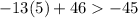
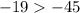
This is true, so x < 7 is indeed a valid solution to the inequality.