Question

PLEASE HELP:
LOOK AT THE ATTACHMENT
PLEASE HELP!!!!!!!
100 PTS

Answer 1

`y \geq (1)/(2) x`.

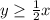Explanation:

1. Find two points.

Looking at the graph you can easily take 2 points that this inequality passes through:

• Point 1: (0, 0)

• Point 2: (2, 1)

Check the attached image to see the selected points highlighted on the graph.

• Use the theory for linear equations to form the expression of the inequality.

Keep in mind that we'll be working with the inequality as if it was an equation on these steps and then we'll select the proper inequality symbol for it.

2. Find the slope

`m=(y_(2)- y_(1) )/(x_(2) -x_(1) ) \\ \\m=((1)-(0))/((2)-(0))\\ \\m=(1)/(2)`

3. Create the formula.

`y-y_(1) =m(x-x_(1) )\\ \\y-(0) =((1)/(2) )(x-(0))\\ \\y=(1)/(2) x`

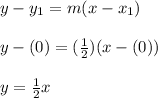
4. Apply the proper symbol.

Now if we look at the graph, the blue shaded part of it indicates the values that this inequality accepts. As you can see, it has a minimum height that goes through the line of the equation we just calculated. Also, the border line is a continuous line. Therefore, the appropiate symbol to add to this inequality should be the greater or equal than symbol (≥). If the line was dashed, the correct symbol would be greater than (>). After applying the symbol, the inequality should look like this:

`y \geq (1)/(2) x`

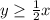
Check the second attached image to see the graphed inequality.