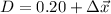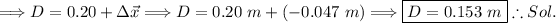Question

Two very large parallel metal plates, separated by 0.20 m, have a potential difference of 12V. An electron is released from rest at a location a distance d from the negative plate.

(a) Describe the motion of the electron after its release in as much detail as possible.
(b) At what distance from the positive plate, will the electron have a speed of 1 x 10^6 m/s?

Answer 1

Given that two large parallel plates are separated by 0.20 m and that the potential difference is 12V.

(a) Describe the motion of an electron released from rest at a distance "d" from the negative plate.

(b) What distance from the positive plate will the electron have a speed of 1 x 10^6 m/s?

For part (a):

The magnitude of an electric field can be given as
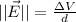`||\vec E||=(\Delta V)/(d)`, where "ΔV" is the potential difference and "d" is the distance between the plates.

So,
`||\vec E||=(12 \ V)/(0.20 \ m) \Longrightarrow \boxed=60 \ (N)/(C)`

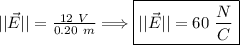
An electric field is created between the plates pointing from positive towards negative. We know that negative charges accelerate opposite the direction of electrical fields. So the electron placed "d" meters away from the negative plate will accelerate towards the positive plate at a constant rate.

For part (b):

We know that...

- the charge of an electron is
`\bold{-1.602 *10^(-19) \ C}`.

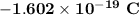- the mass of an electron is
`\bold{9.11 *10^(-31) \ kg}`.

-
`\vec F_e=q\vec E`

-
`\vec F =m\vec a`

`\Longrightarrow \vec F_e=(-1.602 *10^(-19) \ C)(60 \ (N)/(C) }) \Longrightarrow \boxed{\vec F_e= -9.612 *10^(-18) \ N}`

`\Longrightarrow \vec F =m\vec a \Longrightarrow \vec a=(\vec F)/(m) \Longrightarrow \vec a=(-9.612 *10^(-18))/(9.11 *10^(-31) \ kg) \Longrightarrow \boxed{\vec a=-1.06 *10^(13) \ m/s^2}`

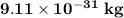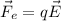
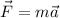
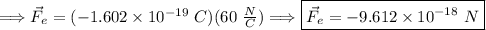
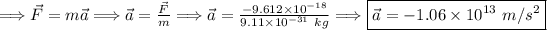
Kinematic Equation:
`\vec v_f^2=\vec v_0^2+2\vec a \Delta \vec x`

`\Longrightarrow 1 *10^(12) \ m^2/s^2=-2.11 *10^(13) \ m/s^2 \Delta \vec x \Longrightarrow \Delta \vec x= (1 *10^(12) \ m^2/s^2)/(-2.12 1*10^(13) \ m/s^2)`

`\Longrightarrow \boxed{\Delta \vec x= -0.047 \ m}`

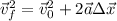
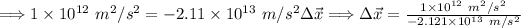
The distance from the positive plate we'll call, "D."

`D=0.20+\Delta \vec x`

`\Longrightarrow D=0.20+\Delta \vec x \Longrightarrow D=0.20 \ m+(-0.047 \ m) \Longrightarrow \boxed{D=0.153 \ m} \therefore Sol.`