Question

Let log,4=3; log,C=2; log, D=5
What is the value of Logb A^3D^4/C^2 ?

Answer 1

D. 25

Explanation:

To find the value of the given logarithmic expression, first rewrite the expression use log laws.

`\boxed{\begin{minipage}{7cm}\underline{Log Laws}\\\\Product law: \quad $\log_axy=\log_ax + \log_ay$\\\\Power law: $\quad\;\;\: \log_ax^n=n\log_ax$\\\\Quotient law:\quad$\log_a \left((x)/(y)\right)=\log_ax - \log_ay$\\\end{minipage}}`

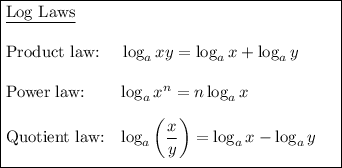
Apply the quotient law, followed by the product law, and finally the power law:

`\begin{aligned}\implies \log_b(A^3D^4)/(C^2) &=\log_b A^3D^4 - \log_b C^2\\& =\log_b A^3+ \log_bD^4 - \log_b C^2\\& =3\log_b A+ 4\log_bD - 2\log_b C\end{aligned}`

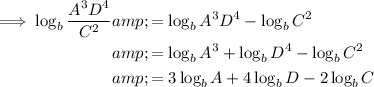
Given:

• 
  `\log_bA=3`

• 
  `\log_bC=2`

• 
  `\log_bD=5`

Substitute the given values into the rewritten expression:

`\begin{aligned}\implies \log_b(A^3D^4)/(C^2) &=3\log_b A+ 4\log_bD - 2\log_b C\\&=3(3)+ 4(5) - 2(2)\\&=9+20-4\\&=29-4\\&=25\end{aligned}`

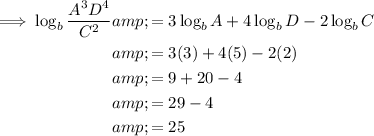
Therefore, the value of the logarithmic expression is 25.