Question #14:
Find the work done by the force field,
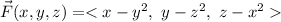 ,
,
on a particle that moves along the line segment from (0,0,1) to (3,1,0).
The parametrized form of a line is given as,
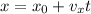
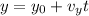
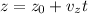
Where
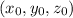 is a point the line passes through and
is a point the line passes through and
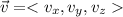 is the direction of the line.
is the direction of the line.
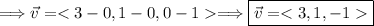
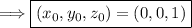
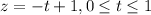
This would imply that,
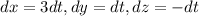
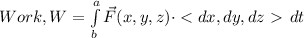
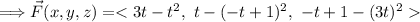
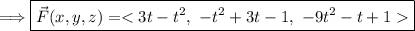
![\Longrightarrow W=\int\limits^1_0 { [ < 3t-t^2, \ -t^2+3t-1, \ -9t^2-t+1 > \cdot} < 3,1,-1 > ] \,dt](https://img.qammunity.org/2024/formulas/mathematics/college/u95sca4kb5umm5vdf8uey9rm78fe0yhu9j.png)
![\Longrightarrow W=\int\limits^1_0 { [( 3t-t^2)(3)+(-t^2+3t-1)(1)+(-9t^2-t+1)(-1) ] \,dt](https://img.qammunity.org/2024/formulas/mathematics/college/n9b8jrw34pq5s9gvak2wjeq78h9pmy5xgy.png)
![\Longrightarrow W=\int\limits^1_0 { [ 9t-3t^2-t^2+3t-1+9t^2+t-1 ] \,dt](https://img.qammunity.org/2024/formulas/mathematics/college/pi0am98db3rtou63t4xdtnxko8cqvkrp98.png)
![\Longrightarrow W=\int\limits^1_0 { [5t^2+13t-2 ] \,dt](https://img.qammunity.org/2024/formulas/mathematics/college/jxjwmyw8vx6gbp3479s2crznhmnmlt9a5r.png)
Using the power rule to integrate:
![(d)/(dx)[x^n]=nx^(n-1)](https://img.qammunity.org/2024/formulas/mathematics/college/v3xt7667nbeq722yddd7lnsughm2ln87d9.png)
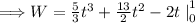
![\Longrightarrow W=[(5)/(3)(1)^3+(13)/(2)(1)^2-2(1)]-[0]](https://img.qammunity.org/2024/formulas/mathematics/college/s259bk3u9yp5y277sis2apkpv1xfwb6vt7.png)
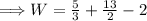
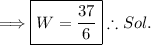
Question #15:
Given:
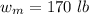
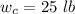
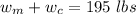
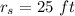
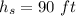
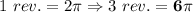
Find:
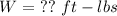
Equation:
![W=\int\ {\vec F \cdot } \, d\vec r \Longrightarrow W=\int\ {[\vec F(\vec r(t)) \cdot r'(t)}]dt](https://img.qammunity.org/2024/formulas/mathematics/college/yf1z5728fk9nosk2hz7tjvdt09iu9spbrk.png)
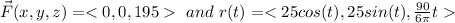
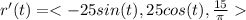
![\Longrightarrow W=\int\ {[\vec F(\vec r(t)) \cdot r'(t)}]dt](https://img.qammunity.org/2024/formulas/mathematics/college/7yltr95kcfu871v71tj7wnp23g9qa53hn7.png)
![\Longrightarrow W=\int\ {[ < 0,0,195 > \cdot < -25sin(t),25cos(t),(15)/(\pi) > ]dt](https://img.qammunity.org/2024/formulas/mathematics/college/w25dfzpc8z68ed4w38j6c0pplrzd7g0mga.png)
![\Longrightarrow W=\int\ {[ (195)((15)/(\pi)) ]dt](https://img.qammunity.org/2024/formulas/mathematics/college/tuif2y9ssc3u9rfzlkj9d0k6hfnieesndc.png)
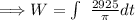
Limits:
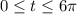
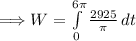
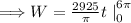
![\Longrightarrow W= [{(2925)/(\pi)(6\pi)]-[0]](https://img.qammunity.org/2024/formulas/mathematics/college/15k2zrndf45bxorlx7nt987o04ts3ua14h.png)
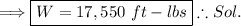
Let me know if these were correct! As I strive to give the most accurate answers! Thank you.