Question

PLEASE HURRY DUE TONIGHT

Mary is babysitting a 4-year-old. The little boy wants to play in the kiddie pool in the backyard. Mary knows that using the hose that is near the kiddie pool will take 30 minutes to fill up. The little boy has already asked 17 times if the pool is ready but she hasn't even turned on the water yet. Mary also knows that the hose from the front yard works faster and can fill the pool in 1/2 the time as the hose in the back yard. If she can use both hoses at the same time, how long will it take for the pool to fill up?


(PLEASE SHOW YOUR WORK)(I saw other people get 7.5 min and 75 min but those answers are incorrect.)


A. 5 minutes

B. 10 minutes

C. 22.5 minutes

Answer 1

We are given that a hose in the front yard can fill the pool in 30 minutes and a hose in the back yard can fill it in half the time (so 15 minutes). We are asked to find the time, we'll call "t," it takes for both hoses together to fill up the pool.

We can create a rational equation,
`(1)/(30)+(1)/(15)=(1)/(t)`. Solve to "t"

`(1)/(30)+(1)/(15)=(1)/(t) \Longrightarrow (1)/(30)+(1)/(15)*(2)/(2) =(1)/(t) \Longrightarrow (1)/(30)+(2)/(30) =(1)/(t) \Longrightarrow (3)/(30) =(1)/(t)`

`\Longrightarrow (1)/(t)=(3)/(30) \Longrightarrow (1)/(t)=(1)/(10) \Longrightarrow \boxed{t=10 \ min}`

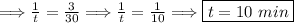
Thus, b is the correct option.