Answer:
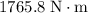 , assuming that
, assuming that
 and that the vehicle is on a level surface.
and that the vehicle is on a level surface.
Step-by-step explanation:
The weight of this
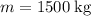 vehicle is
vehicle is
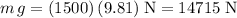 .
.
Under the assumptions, the normal force from the ground on this vehicle would be equal to its weight,
 . Since this normal force would be evenly split between the wheels, the normal force on each wheel would be
. Since this normal force would be evenly split between the wheels, the normal force on each wheel would be
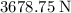 .
.
As long as the wheels aren't spinning or slipping, friction between the wheels and the ground is considered "static". This type of friction is the same as that on a box that is stationary on a slope (static), and not the same as the friction on a box sliding along the slope (kinetic).
To find the maximum static friction on each wheel, multiply normal force by the coefficient of static friction
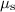 :
:
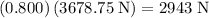 .
.
At a distance of
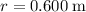 from the axis of rotation, the maximum torque on each wheel from static friction would be:
from the axis of rotation, the maximum torque on each wheel from static friction would be:
 .
.