Question

Kaylee is 1.45 meters tall. At 3 p.m., she measures the length of a tree's shadow to be 39.55 meters. She stands 34.2 meters away from the tree, so that the tip of her shadow meets the tip of the tree's shadow. Find the height of the tree to the nearest hundredth of a meter.

Answer 1

The height of the tree is approximately 14.15 meters.

To find this, we used the concept of similar triangles, establishing a proportion between Kaylee's height, her shadow, and the tree's shadow. Solving the proportion yielded the tree's height as 14.15 meters.

Explanation:

In order to determine the height of the tree, we can use the concept of similar triangles formed by Kaylee, her shadow, and the tree's shadow. Let's denote the height of Kaylee as
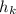`\(h_k\)`, the height of the tree as
`\(h_t\)`, the length of Kaylee's shadow as
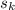`\(s_k\)`, and the length of the tree's shadow as
`\(s_t\)`.

The triangles formed by Kaylee and the tree are similar, so we can set up the following proportion:

`\[ (h_k)/(s_k) = (h_t)/(s_t) \]`

We know that Kaylee's height is 1.45 meters, the length of her shadow is the distance from her to the tree (34.2 meters), and the length of the tree's shadow is given as 39.55 meters. Plugging in these values, we can solve for the height of the tree
`(\(h_t\))` :

`\[ (1.45)/(34.2) = (h_t)/(39.55) \]`

Now, solve for
`\(h_t\)`:

`\[ h_t = (1.45 * 39.55)/(34.2) \]`

Calculating this expression gives us the height of the tree, which is approximately 14.15 meters.

This method utilizes the geometric relationship between similar triangles, allowing us to find the height of the tree based on the known measurements of Kaylee's height and the lengths of the shadows. The final answer, 14.15 meters, represents the height of the tree to the nearest hundredth of a meter.

Answer 2

Explanation:

We can use the ratios of similar triangles to solve this problem. Let's call the height of the tree "h". Then, we have two similar right triangles:

Kaylee's triangle: the height is 1.45 meters, the length of the shadow is 34.2 meters, and the angle between the height and the shadow is theta.

Tree's triangle: the height is h meters, the length of the shadow is 39.55 meters, and the angle between the height and the shadow is also theta.

Using these two triangles, we can set up the following proportion:

h / 39.55 = 1.45 / 34.2

Cross-multiplying, we get:

h * 34.2 = 39.55 * 1.45

Simplifying:

h = (39.55 * 1.45) / 34.2

h = 1.68176

So the height of the tree is approximately 1.68 meters (to the nearest hundredth of a meter).