Question

Calculate the area of the shaded region in the given figure.

Answer 1

Answer: =53.46 in²

Explanation:

You need to first find the area of the circle then subtract the area of the polygon inside the circle.

We do not have the radius of the circle so we need to find the radius and apothem of the polygon first.

A(polygon) = 1/2 a P 8 sided figure(octagon)

a=apothem (that is the center of the shape to the center of a side creating a right angle

P=perimeter= 10(8) =80

to find the apothem you need to find the angle of the vertex and take half of it to make a right triangle so you can use trig to find a (picture of apothem attached.

To find the angle, all external angles add to 360 so 360/8 = 45 so the internal angles are 180-45=135

half of that for the right triangle is 67.5

half the side is 5 for the Right triangle, now use trig to find to find a

tan 67.5=
`(a)/(5)`

a=5tan67.5

a=12.07

A(octagon)=1/2(12.07)(80

=482.84

now to find the circle we need to find radius of octagon which is same radius for circle

use trig to find hypotenuse of that triangle

cos 67.5 = 5/r

r=5/cos67.5

r=13.07

A(circle)=
`\pi`r²

=
`\pi 13.07^(2)`

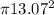
=536.30

A(shaded)= A(circle)-A(octagon)

=536.30-482.84

=53.46 in²