Question

Please answer in detail

Answer 1

The area of triangle APB is 240 m².

Explanation:

We are told that PA and PB are equal in length. Therefore, triangle APB is an isosceles triangle with base AB.

As PQ is perpendicular to the base (signified by the right angle symbol), point Q is the midpoint of AB. This means that:

• The length of AQ is equal to the length of QB.
• PQ is the altitude (height) of triangle APB.

As triangle PQB is a right triangle, use Pythagoras Theorem to find the length of QB:

`\implies PQ^2+QB^2=PB^2`

`\implies 24^2+QB^2=26^2`

`\implies 576+QB^2=676`

`\implies 576+QB^2-576=676-576`

`\implies QB^2=100`

`\implies √(QB^2)=√(100)`

`\implies QB=10`

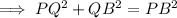
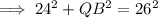
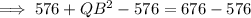
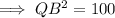
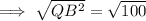
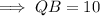
As AQ = QB, and QB is 10 m, then AQ is also 10 m.

Therefore, we can calculate the length of the base AB:

`\begin{aligned}\implies AB &= AQ + QB\\&=10 + 10 \\&= 20\; \sf m\end{aligned}`

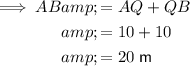
Now we have the length of the base of the triangle and the height of the triangle, we can calculate the area of triangle APB:

`\begin{aligned}\textsf{Area of triangle $APB$}&=(1)/(2) \cdot \sf base \cdot height\\\\&=(1)/(2) \cdot AB \cdot PQ\\\\&=(1)/(2) \cdot 20 \cdot 24\\\\&=10 \cdot 24\\\\&=240\; \sf m^2\end{aligned}`

Therefore, the area of triangle APB is 240 m².