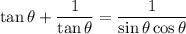Question

Please help urgently! maths trigonometry

Answer 1

Explanation:

`\tan( \alpha ) + (1)/( \tan( \alpha ) )`

`\frac{ { \tan( \alpha ) }^(2) + 1 }{ \tan( \alpha ) }`

use the identity

`{ \tan( \alpha ) }^(2) + 1 = { \sec( \alpha ) }^(2)`

so we have

`\frac{ { \sec( \alpha ) }^(2) }{ \tan( \alpha ) }`

now we use the following id.

`\sec( \alpha ) = (1)/( \cos( \alpha ) ) \: and \: \: \tan( \alpha) = ( \sin( \alpha ) )/( \cos( \alpha ) )`

then, back to what we had

`\frac{ \frac{1}{ { \cos( \alpha ) }^(2) } }{ ( \sin( \alpha ) )/( \cos( \alpha ) ) }`

and finally, this equals to what we wanted to prove

`(1)/( \sin( \alpha ) \cos( \alpha ) )`

Answer 2

See below for proof.

Explanation:

To prove the given trigonometric equation, we can use the following tangent trigonometric identities:

`\boxed{\tan \theta=(\sin \theta)/(\cos \theta)}`
`\boxed{(1)/(\tan \theta)=(\cos \theta)/(\sin \theta)}`

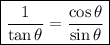
Therefore:

`\tan \theta + (1)/(\tan \theta)=(\sin \theta)/(\cos \theta)+(\cos \theta)/(\sin \theta)`

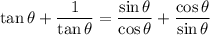
Add the fractions on the right side of the equation:

`\begin{aligned}\tan \theta + (1)/(\tan \theta)&=(\sin \theta)/(\cos \theta)+(\cos \theta)/(\sin \theta)\\\\ &=(\sin \theta \cdot \sin \theta)/(\cos \theta \cdot \sin \theta)+(\cos \theta \cdot \cos \theta)/(\sin \theta \cdot \cos \theta)\\\\ &=(\sin^2 \theta )/(\sin \theta \cos \theta)+(\cos^2 \theta )/(\sin \theta \cos \theta)\\\\&=(\sin^2 \theta + \cos^2\theta)/(\sin \theta \cos\theta)\end{aligned}`

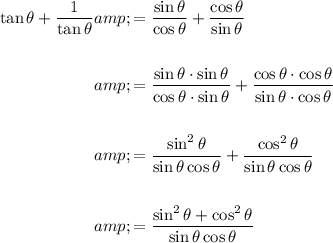
Apply the identity sin²θ + cos²θ = 1:

`\begin{aligned}\tan \theta + (1)/(\tan \theta)&=(\sin \theta)/(\cos \theta)+(\cos \theta)/(\sin \theta)\\\\ &=(\sin \theta \cdot \sin \theta)/(\cos \theta \cdot \sin \theta)+(\cos \theta \cdot \cos \theta)/(\sin \theta \cdot \cos \theta)\\\\ &=(\sin^2 \theta )/(\sin \theta \cos \theta)+(\cos^2 \theta )/(\sin \theta \cos \theta)\\\\&=(\sin^2 \theta + \cos^2\theta)/(\sin \theta \cos\theta)\\\\&=(1)/(\sin \theta \cos\theta)\end{aligned}`

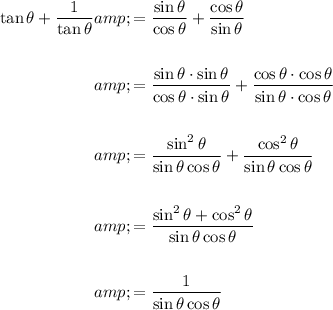
Therefore, we have proved that:

`\tan \theta + (1)/(\tan \theta)=(1)/(\sin \theta \cos\theta)`