Question

If cos A =

of sin A?
Square root of 5 divided by
3
and tan A < 0, what is the value of Sin A?

Answer 1

The answer is a. It may help you to draw a triangle for reference

Answer 2

Answer:
`\tt{a.\fra{2}{3}}`

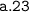
Explanation:

If cos A = sqrt(5)/3 and tan A < 0, we can use the fact that:

sin^2 A + cos^2 A = 1

to find the value of sin A. First, we can square both sides of the equation cos A = sqrt(5)/3 to get:

cos^2 A = 5/9

Then, we can use the identity sin^2 A = 1 - cos^2 A to get:

sin^2 A = 1 - cos^2 A

sin^2 A = 1 - 5/9

sin^2 A = 4/9

Taking the square root of both sides gives us:

sin A = +/- 2/3

However, we know that tan A < 0, which means that the sine and cosine functions have opposite signs in the quadrant where angle A lies. Since cosine is positive (given by cos A = sqrt(5)/3), angle A must lie in either the first or fourth quadrant, where sine is positive or negative, respectively. Therefore, we can eliminate the negative solution and conclude that:

sin A = 2/3