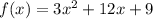Question

The graph of a quadratic function is shown. What is the equation of this function in f(x)=ax^2+bx+c​ form?

Answer 1

`f(x)=3x^2+12x+9`

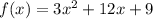
Explanation:

Recall that the factored form of a quadratic is:

`f(x)=a(x-r_(1) )(x-r_(2))`

Where r1 and r2 are the roots of the quadratic.

As shown in the image, the x-intercepts are (-3, 0) and (-1, 0).

Since these are the values of x when y=0, they are the roots of the quadratic equation. Let's plug them in. We get:

`f(x)=a(x-(-3)(x-(-1)=\\f(x)=a(x+3)(x+1)=\\f(x)=a(x^2+4x+3)`

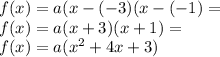
We are given that the point (-2, -3) also belongs to the graph. This means that when x=-2, y=-3. Let's plug in those points and solve for a:

`f(x)=a(x+3)(x+1)=\\-3=a(-2+3)(-2+1)=\\-3=a(1)(-1)=\\-3=-a=\\3=a`

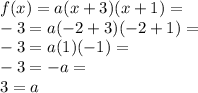
Now, let's go back to the equation:

`f(x)=a(x^2+4x+3)`

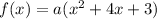
and substitute a with 3, then solve.

`f(x)=a(x^2+4x+3)=\\f(x)=3(x^2+4x+3)=\\f(x)=3x^2+12x+9`

Thus, the equation of this function is
`f(x)=3x^2+12x+9`