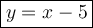Question

NO LINKS!!! URGENT HELP PLEASE!!!

1. Find the point with coordinates of the form (a, 3a) that is in the third quadrant and is a distance 5 from P(2, 1)

(x, y) = ______________

2. Find a formula that expresses the fact that an arbitrary point P(x, y) is on the perpendicular bisector "l" of segment AB.

A(-6, 3), B(8, -11)

Answer 1

1. (-1, -3)

2. y = x - 5

Explanation:

Question 1

To find the values of a where the point (a, 3a) is a distance of 5 units from P(2, 1) use the distance formula.

`\boxed{\begin{minipage}{7.4 cm}\underline{Distance Formula}\\\\$d=√((x_2-x_1)^2+(y_2-y_1)^2)$\\\\\\where:\\ \phantom{ww}$\bullet$ $d$ is the distance between two points. \\\phantom{ww}$\bullet$ $(x_1,y_1)$ and $(x_2,y_2)$ are the two points.\\\end{minipage}}`

Given values:

• d = 5
• (x₁, y₁) = (2, 1)
• (x₂, y₂) = (a, 3a)

Substitute the given values into the distance formula and solve for a:

`\begin{aligned}√((a-2)^2+(3a-1)^2)&=5\\(a-2)^2+(3a-1)^2&=25\\a^2-4a+4+9a^2-6a+1&=25\\10a^2-10a-20&=0\\a^2-a-2&=0\\a^2-2a+a-2&=0\\a(a-2)+1(a-2)&=0\\(a+1)(a-2)&=0\\\\a+1&=0 \implies a=-1\\a-2&=0 \implies a=2\end{aligned}`

Substitute the found values of a into the point coordinate formula, (a, 3a):

`a=-1 \implies (-1,-3)`

`a=2 \implies (2, 6)`

As the point is in the third quadrant, this means that the x and y coordinates are negative.

Therefore, the point with coordinates of the form (a, 3a) that is in the third quadrant and is a distance 5 units from P (2, 1) is:

`\large\boxed{(-1, -3)}`

`\hrulefill`

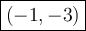
Question 2

The perpendicular bisector of segment AB is the line that passes through the midpoint of AB and is perpendicular to AB.

To find the midpoint of AB, use the midpoint formula.

`\boxed{\begin{minipage}{7.4 cm}\underline{Midpoint between two points}\\\\Midpoint $=\left((x_2+x_1)/(2),(y_2+y_1)/(2)\right)$\\\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are the endpoints.\\\end{minipage}}`

Let (x₁, y₁) = A = (-6, 3)

Let (x₂, y₂) = B = (8, -11)

Substitute the values into the midpoint formula:

`\text{Midpoint of $AB$}=\left((8-6)/(2),(-11+3)/(2)\right)=\left(1,-4\right)`

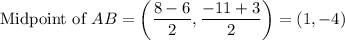
Therefore, the midpoint of AB is (1, -4).

To find the slope of AB, use the slope formula.

`\implies \textsf{slope}\:(m)=(y_2-y_1)/(x_2-x_1)=(-11-3)/(8-(-6))=(-14)/(14)=-1`

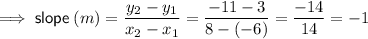
The slope of a line that is perpendicular to AB is the negative reciprocal of the slope of AB.

Therefore, the slope of the line perpendicular to AB is m = 1.

To determine the equation of the perpendicular bisector of AB that passes through the midpoint of AB and is perpendicular to AB, substitute the found slope, m = 1, and the midpoint (1, -4) into the point-slope formula:

`\implies y-y_1=m(x-x_1)`

`\implies y-(-4)=1(x-1)`

`\implies y+4=x-1`

`\implies y=x-5`

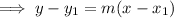
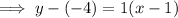
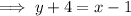
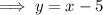
Therefore, the formula that expresses the fact that an arbitrary point P(x, y) is on the perpendicular bisector "l" of segment AB is:

`\large\boxed{y=x-5}`