Question

NO LINKS!! URGENT HELP PLEASE!!!!!

Express in terms of logarithms of x, y, z, or w.

a. log_7(xz)

b. log_7(y/x)

c. log_7(cube root of z)

Answer 1

a.
`\bold{log_7(xz) = log_7(x * z) = log_7(x) + log_7(z)}`

b.
`\bold{log_7((x)/(y)) = log_7(y) - log_7(x)}`

c.
`\bold{log_7(\sqrt[3]{7} ) = log_7(z^{(1)/(3)}) = (1)/(3)log_7(z)}`

Explanation:

let me provide an explanation for each of the expressions.

• a. To express log_7(xz) in terms of logarithms of x and z, we use the logarithmic property that states log(a * b) = log(a) + log(b). Applying this property, we get:

`\bold{log_7(xz) = log_7(x * z) = log_7(x) + log_7(z)}`

• b. To express log_7(y/x) in terms of logarithms of y and x, we use the logarithmic property that states log(a / b) = log(a) - log(b). Applying this property, we get:

`\bold{log_7((x)/(y)) = log_7(y) - log_7(x)}`

• c. To express log_7(cube root of z) in terms of the logarithm of z, we use the logarithmic property that states log(a^(n)) = n * log(a), where n is a constant. Applying this property, we get:

`\bold{log_7(\sqrt[3]{7} ) = log_7(z^{(1)/(3)}) = (1)/(3)log_7(z)}`

Therefore, we can express each of the given expressions in terms of logarithms of x, y, z, or w using the logarithmic properties mentioned above.

Answer 2

`\textsf{a.} \quad \log_7(x) + \log_7(z)`

`\textsf{b.} \quad \log_7(y) - \log_7(x)`

`\textsf{c.} \quad (1)/(3)\log_7(z)`

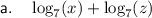
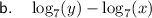
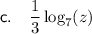
Explanation:

We can express the given logarithmic expressions in terms of x, y, z or w by using the laws of logarithms.

`\hrulefill`

Part (a)

`\boxed{\begin{array}{c}\underline{\textsf{Product law}}\\\\ \log_a(bc)=\log_a(b) + \log_a(c)\\\end{array}}`

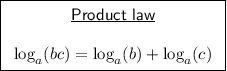
By using the log product law, we can express log₇(xz) as:

`\log_7(xz) =\log_7(x) + \log_7(z)`

`\hrulefill`

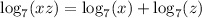
Part (b)

`\boxed{\begin{array}{c}\underline{\textsf{Quotient law}}\\\\\log_a \left((b)/(c)\right)=\log_a(b) - \log_a(c)\end{array}}`

By using the log quotient law, we can express log₇(y/x) as:

`\log_7 \left((y)/(x)\right)=\log_7(y) - \log_7(x)`

`\hrulefill`

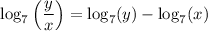
Part (c)

`\boxed{\begin{array}{c}\underline{\textsf{Power law}}\\\\\log_ax^n=n\log_ax\end{array}}`

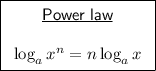
By using the log power law, we can express log₇(∛z) as:

`\begin{aligned}\log_7 \left(\sqrt[3]{z}\right)&=\log_7 \left(z^{(1)/(3)\right) \\&=(1)/(3)\log_7(z)\end{aligned}`