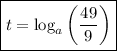Question

NO LINKS!! URGENT HELP PLEASE!!!

1.Change to exponential form

a. ln w = 7 + 6x


2. Solve for t using a logarithm with base a

a. 3a^(t/2) = 7

Answer 1

1. w =
`\bold{e^(7+6x)}`

2.
`\bold{t = 2(log_a(7) - log_a(3))}`

Explanation:

1.

a. The exponential form of a logarithmic equation is given by:

`\bold{log_a(b) }`= c is equivalent to
`a^c = b`

Using this rule, we can rewrite the equation:

ln w = 7 + 6x as w =
`\bold{e^(7+6x)}`

Therefore, the exponential form of the given equation is w =
`\bold{e^(7+6x)}`

2.

a. To solve for t using a logarithm with base a, we can take the logarithm of both sides of the equation:

`\bold{3a^(t)/(2) = 7 }\\\bold{log_a3a^(t)/(2)= log_a(7)}`

Using the rule of logarithms that log_a(b^n) = n*log_a(b), we can simplify the left side:

`\bold{log_a(3) +(t)/(2) log_a(a) = log_a(7)}`

Since log_a(a) = 1 for any base a, we can simplify the expression further:

`\bold{log_a(3) + (t)/(2)*1= log_a(7)}`

Now we can solve for t by isolating it on one side of the equation:

`\bold{ (t)/(7) = (log_a(7) - log_a(3))} \\ \bold{t = 2(log_a(7) - log_a(3))}`

Therefore, the solution for t using a logarithm with base a is
`\bold{t = 2(log_a(7) - log_a(3))}`

Answer 2

`\textsf{1.} \quad w = e^(7 + 6x)`

`\textsf{2.} \quad t= \log_a\left((49)/(9)\right)`

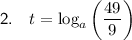
Explanation:

Question 1

Exponential form is a way to represent a number using an exponent, where the base is raised to a power.

The natural logarithm function is the inverse of the exponential function:

`\boxed{\ln x=y \iff x=e^y}`

Therefore we can use this definition to change the given equation to exponential form:

`\begin{aligned}\ln w & = 7 + 6x\\\\e^(\ln w) & = e^(7+6x)\\\\w&=e^(7+6x)\end{aligned}`

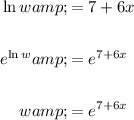
Therefore, the exponential form of the equation is:

`w = e^(7 + 6x)`

`\hrulefill`

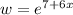
Question 2

To solve for t using a logarithm with base a, begin by taking the logarithm of both sides of the equation with base a:

`\log_a (3a^{(t)/(2)})=\log_a(7)`

`\textsf{Apply the log product law:} \quad \log_axy=\log_ax + \log_ay`

`\log_a (3)+\log_a(a^{(t)/(2)})=\log_a(7)`

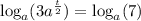
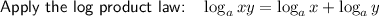
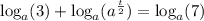
Subtract logₐ(3) from both sides of the equation:

`\log_a (3)+\log_a(a^{(t)/(2)})-\log_a (3)=\log_a(7)-\log_a (3)`

`\log_a(a^{(t)/(2)})=\log_a(7)-\log_a (3)`

`\textsf{Apply the log quotient law:} \quad \log_ax - \log_ay=\log_a \left((x)/(y)\right)`

`\log_a(a^{(t)/(2)})=\log_a\left((7)/(3)\right)`

`\textsf{Apply the log power law:} \quad \log_ax^n=n\log_ax`

`(t)/(2)\log_a(a)=\log_a\left((7)/(3)\right)`

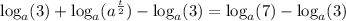
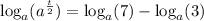
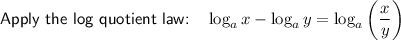
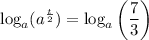
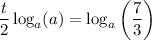
Apply the log law: logₐ(a) = 1

`(t)/(2)(1)=\log_a\left((7)/(3)\right)`

`(t)/(2)=\log_a\left((7)/(3)\right)`

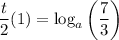
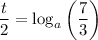
Multiply both sides of the equation by 2:

`2 \cdot (t)/(2)=2 \cdot \log_a\left((7)/(3)\right)`

`t=2 \log_a\left((7)/(3)\right)`

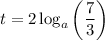
Finally, apply the log power law:

`t= \log_a\left((7)/(3)\right)^2`

`t= \log_a\left((7^2)/(3^2)\right)`

`t= \log_a\left((49)/(9)\right)`

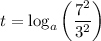
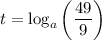
Therefore, the solution for t in terms of logarithm with base a is:

`\boxed{t= \log_a\left((49)/(9)\right)}`