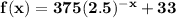Question

NO LINKS!! URGENT HELP PLEASE!!!

1. Find an exponential function of the form f(x) = ba^-1 + c that has the given horizontal asymptote and y-intercept and passes through P

y = 33; y-intercept 408; P(2, 93)

Answer 1

`\bold{f(x) = 375(2.5)^(-x)+ 33}`

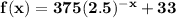
Explanation:

An exponential function of form f(x) = ba^(-x) + c has a horizontal asymptote of y = c as x approaches infinity, and a y-intercept of (0, b + c). We can use the given information to set up a system of equations and solve for the unknowns.

The horizontal asymptote is given as y = 33, so we have:

c = 33

The y-intercept is given as (0, 408), so we have:

b + c = 408

Substituting c = 33, we get:

b + 33 = 408

b = 375

So the function we're looking for is of the form:

`\bold{f(x) = 375a^(-x)+ 33}`

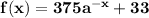
To find a, we use the fact that the function passes through P(2, 93):

93 = 375a^(-2) + 33

60 = 375a^(-2)

a^2 = 375/60

a^2 = 6.25

a =
`√(6.25 ) =2.5`

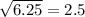
Therefore, the exponential function that satisfies the given conditions is:

`\bold{f(x) = 375(2.5)^(-x)+ 33}`