Question

Find the solution to the system of equations below.
2y = 2x - 8
2x + y = 5

Answer 1

The solution to the system of equations is:

• (x, y) = (3, -1)

The graph is attached below.

Explanation:

Given the system of equations

`2y = 2x - 8`

`2x + y = 5`

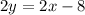
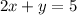
Let us solve the system of equations using the elimination method

`\begin{bmatrix}2y=2x-8\\ 2x+y=5\end{bmatrix}`

Arrange equation variables for elimination

`\begin{bmatrix}2y-2x=-8\\ y+2x=5\end{bmatrix}`

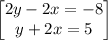
Multiply y + 2x = 5 by 2: 2y + 4x = 10

`\begin{bmatrix}2y-2x=-8\\ 2y+4x=10\end{bmatrix}`

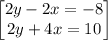
subtracting the equations

`2y+4x=10`

`-`

`\underline{2y-2x=-8}`

`6x=18`

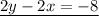
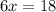
solve 6x = 18 for x

`6x=18`

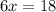
Divide both sides by 6

`(6x)/(6)=(18)/(6)`

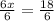
simplify

`x=3`

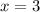
For 2y - 2x = -8 plug in x = 3

`2y-2\cdot \:3=-8`

`2y-6=-8`

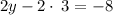
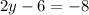
Add 6 to both sides

`2y-6+6=-8+6`

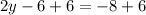
Simplify

`2y=-2`

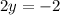
Divide both sides by 2

`(2y)/(2)=(-2)/(2)`

Simplify

`y=-1`

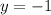
Therefore, the solution to the system of equations is:

• (x, y) = (3, -1)

The graph is attached below.