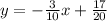Question

Rewrite the following equation in slope-intercept form 6x+20y=17​

Answer 1

`y =- (3)/(10) x + (17)/(20)`

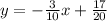
Explanation:

Pre-Solving

We are given the line 6x+20y=17, and we want to write it in slope-intercept form.

Slope-intercept form is given as y=mx+b, where m is the slope and b is the value of y at the y-intercept, hence the name.

Solving

As we can see, in slope-intercept form, y is by itself on one side. So, we should solve the equation for y.

To do that, we can start by subtracting 6x from both sides.

6x + 20y = 17

-6x -6x

_________________

20y = -6x + 17

Now, we should divide both sides by 20 to isolate y.

20y = -6x + 17

÷20 ÷20

_______________

`y=-(6)/(20) x + (17)/(20)`

This can be simplified to:

`y =- (3)/(10) x + (17)/(20)`