Answer:
Approximately
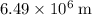 .
.
Step-by-step explanation:
Look up the Gravitational Constant:
 .
.
Assume that the net force
 on this rocket is equal to the gravitational attraction from the Earth (i.e., there is no other force on this rocket.) This force would be equal to:
on this rocket is equal to the gravitational attraction from the Earth (i.e., there is no other force on this rocket.) This force would be equal to:
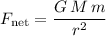 ,
,
Where:
 is the gravitational field strength,
is the gravitational field strength,
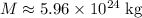 (as given) is the mass of the Earth,
(as given) is the mass of the Earth,
 is the mass of this rocket, and
is the mass of this rocket, and
 is the orbital radius that needs to be found.
is the orbital radius that needs to be found.
Since the rocket is in a circular orbit of radius
 with a tangential speed of
with a tangential speed of
 , acceleration would be equal to:
, acceleration would be equal to:
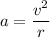 .
.
The net force on this rocket would be equal to:
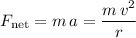 .
.
Equate the two expressions for the net force on the rocket (from the gravitational force and from the centripetal motion) to obtain:
 .
.
Simplify and solve this equation for orbital radius
 :
:
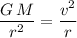 .
.
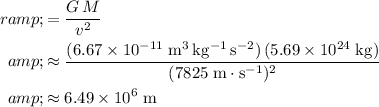 .
.