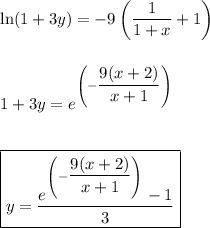Question

What is the particular solution to the differential equation?

Answer 1

y = (1/3)(e^(-9(x+2)/(x+1)) -1)

Explanation:

You want the particular solution to the differential equation ...

y' = 3(1+3y)/(1+x)^2 with y(-2) = 0

Separation of variables

The differential equation can be rewritten as ...

`(dy)/(3(1+3y))=(dx)/((1+x)^2)`

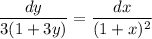
We can define u = 1+3y, then du = 3 and the left side becomes ...

dy/(3(1+3y)) = (1/9)du/u

and its integral is ...

∫(1/9)du/u = (1/9)ln(u) = (1/9)ln(1 +3y)

The integral of the right side is ...

`\int{(1+x)^(-2)}\,dx=-(1+x)^(-1)+C`

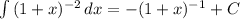
Result

Then the result of integrating both sides of this rewritten differential equation is ...

`(1)/(9)ln((1+3y))=-(1)/(1+x)+C`

The boundary condition can be used to find C:

`(\ln(1+3\cdot0))/(9)=-(1)/(1-2)+C\\\\0=1+C\\\\C=-1`

Particular solution

Solving this equation for y, we get ...

`\ln(1+3y)=-9\left((1)/(1+x)+1\right)\\\\\\1+3y=e^{\left(-(9(x+2))/(x+1)\right)}\\\\\\\boxed{y=\frac{e^{\left(-(9(x+2))/(x+1)\right)}-1}{3}}`