Question

WORTH 45!!! the number 203 is which term in the arithmetic sequence -7, -2, 3, … ?

Answer 1

43rd term

Explanation:

Given arithmetic sequence:

• -7, -2, 3, ...

We can use the formula for the nth term of an arithmetic sequence to find which term the number 203 corresponds to in the given arithmetic sequence.

The formula for the nth term of an arithmetic sequence is:

`\boxed{a_n = a_1 + (n-1)d}`

where:

• a₁ is the first term.
• d is the common difference between terms.
• n is the position of the nth term.

For the given sequence, we know that the first term is a₁ = -7.

The common difference is d = 5, since each term is 5 more than the previous term.

Substitute these values into the formula to create an equation for the nth term:

`\begin{aligned} \implies a_n &= -7 + (n-1)5\\&=-7+5n-5\\&=5n-12 \end{aligned}`

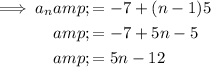
To find the position of number 203 in the sequence, substitute aₙ = 203 into the equation for the nth term and solve for n:

`\begin{aligned} a_n &= 203\\ \implies5n-12&=203\\5n-12+12&=203+12\\5n&=215\\(5n)/(5)&=(215)/(5)\\n&=43 \end{aligned}`

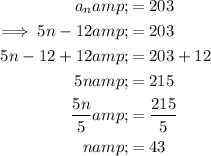
Therefore, the number 203 corresponds to the 43rd term in the given arithmetic sequence.