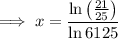Question

Solve the following equation for x, giving your answer in the form lnp/lnq

2 × 5^(3x+2) = 6 x 7^(1-2x)

Answer 1

`x=(\ln \left((21)/(25)\right))/(\ln 6125)`

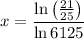
Explanation:

Given equation:

`2 \cdot 5^(3x+2) = 6 \cdot 7^(1-2x)`

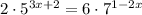
Divide both sides of the equation by 2:

`\implies 5^(3x+2) = 3 \cdot 7^(1-2x)`

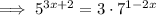
Take natural logs of both sides:

`\implies \ln \left(5^(3x+2)\right) = \ln \left(3 \cdot 7^(1-2x)\right)`

`\textsf{Apply the product law:} \quad \ln xy=\ln x + \ln y`

`\implies \ln 5^(3x+2) = \ln 3 + \ln 7^(1-2x)`

`\textsf{Apply the power law:} \quad \ln x^n=n \ln x`

`\implies (3x+2)\ln 5 = \ln 3 + (1-2x)\ln7`

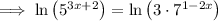
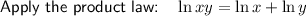
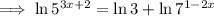
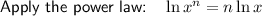
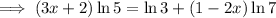
Expand:

`\implies 3x\ln 5+2\ln 5=\ln 3+\ln7-2x\ln7`

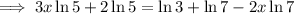
Collect the terms in x on the left side and the constants on the right side of the equation:

`\implies 3x\ln 5+2x\ln7=\ln 3+\ln7-2\ln 5`

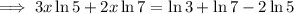
Factor out the common term x on the left side:

`\implies x(3\ln 5+2\ln7)=\ln 3+\ln7-2\ln 5`

`\textsf{Apply the power law:} \quad n \ln x=\ln x^n`

`\implies x(\ln 5^3+\ln7^2)=\ln 3+\ln7-\ln 5^2`

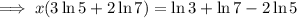
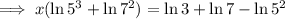
Simplify:

`\implies x(\ln 125+\ln 49)=\ln 3+\ln7-\ln 25`

`\textsf{Apply the product law:} \quad \ln x + \ln y=\ln xy`

`\implies x(\ln (125 \cdot 49))=\ln (3\cdot 7)-\ln 25`

`\implies x(\ln 6125)=\ln 21-\ln 25`

`\textsf{Apply the quotient law:} \quad \ln x - \ln y=\ln \left((x)/(y)\right)`

`\implies x(\ln 6125)=\ln \left((21)/(25)\right)`

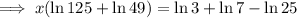
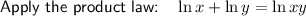
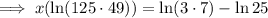
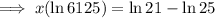
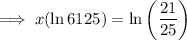
Divide both sides of the equation by ln 6125:

`\implies x=(\ln \left((21)/(25)\right))/(\ln 6125)`