Question

The circumference of a circle is 7π in. What is the area, in square inches? Express your answer in terms of π.

Answer 1

`(49)/(4)\pi=12.25\pi \; \sf in^2`

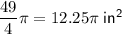
Explanation:

To find the area of the circle with a circumference of 7π inches, first need to find the radius of the circle.

The formula for the circumference of a circle is:

`\boxed{C = 2 \pi r}`

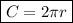
where r is the radius of the circle.

If the circumference of a circle is 7π inches, substitute C = 7π into the formula and solve for the radius, r:

`\begin{aligned}\implies 2\pi r&=7\pi\\\\(2\pi r)/(2\pi)&=(7\pi)/(2\pi)\\\\r&=(7)/(2)\; \sf in\end{aligned}`

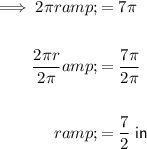
The formula for the area of a circle is:

`\boxed{A=\pi r^2}`

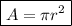
where r is the radius of the circle.

Substitute the found value of r into the area formula to find the area of the circle:

`\begin{aligned}\implies \sf Area&=\pi r^2\\\\&=\pi \cdot \left((7)/(2)\right)^2\\\\&=\pi \cdot \left((7^2)/(2^2)\right)\\\\&=\pi \cdot \left((49)/(4)\right)\\\\&=(49)/(4)\pi \\\\&=12.25\pi \sf \; in^2\end{aligned}`

Therefore, the area of the circle in terms of π is (49/4)π square inches.