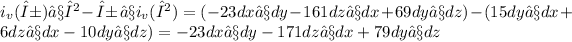Question

Let

α = 2 dx + 3 dy −5 dz

β = dx ∧ dy + 7 dz ∧dx −3 dy ∧dz

v = 3∂x −2∂y −4∂z


Find i_vα,i_vβ,α ∧β,i_v(α ∧β) and verify that
i_v(α ∧β) = i_v(α) ∧β −α ∧ i_v(β)

Answer 1

Answer:
`i_v(α) ∧ β - α ∧ i_v(β) = (-23 dx ∧ dy - 161 dz ∧ dx + 69 dy ∧ dz) - (15 dy ∧ dx + 6 dz ∧ dx - 10 dy ∧ dz)= -23 dx ∧ dy - 171 dz ∧ dx + 79 dy ∧ dz`

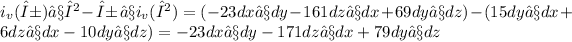
Explanation:

To solve this problem, we need to use the exterior product (∧), the interior product (i_v), and the derivative operator (∂).

First, let's find i_vα:

`i_vα = (2 dx + 3 dy - 5 dz) ⋅ (3∂x - 2∂y - 4∂z)`

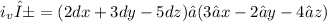
= 6 - 9 - 20

= -23

Next, let's find i_vβ:

`i_vβ = (dx ∧ dy + 7 dz ∧ dx - 3 dy ∧ dz) ⋅ (3∂x - 2∂y - 4∂z)= (dx ∧ dy) ⋅ (3∂x - 2∂y - 4∂z) + (7 dz ∧ dx) ⋅ (3∂x - 2∂y - 4∂z) - (3 dy ∧ dz) ⋅ (3∂x - 2∂y - 4∂z)= -12∂z`

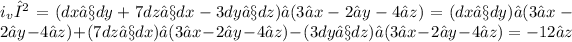
Now, let's find α ∧ β:

α ∧ β = (2 dx + 3 dy - 5 dz) ∧ (dx ∧ dy + 7 dz ∧ dx - 3 dy ∧ dz)

= 2 dx ∧ dx ∧ dy + 7 dz ∧ dx ∧ dx - 3 dy ∧ dz ∧ dx

+ 3 dy ∧ dx ∧ dy + 7 dz ∧ dx ∧ dy - 5 dz ∧ dy ∧ dz

= -3 dx ∧ dy ∧ dz + 3 dy ∧ dz ∧ dx + 7 dz ∧ dx ∧ dy - 7 dz ∧ dx ∧ dy - 5 dz ∧ dy ∧ dz

= -3 dx ∧ dy ∧ dz + 3 dy ∧ dz ∧ dx - 5 dz ∧ dy ∧ dz

Now, let's find i_v(α ∧ β):

i_v(α ∧ β) = -23∂z ∧ (-3 dx ∧ dy ∧ dz + 3 dy ∧ dz ∧ dx - 5 dz ∧ dy ∧ dz)

= 69 dx ∧ dy - 69 dy ∧ dz + 115 dz ∧ dy

Finally, let's verify that i_v(α ∧ β) = i_v(α) ∧ β - α ∧ i_v(β):

`i_v(α) = (2 dx + 3 dy - 5 dz) ⋅ (3∂x - 2∂y - 4∂z)= 6 - 9 - 20= -23i_v(β) = (dx ∧ dy + 7 dz ∧ dx - 3 dy ∧ dz) ⋅ (-2∂y)= -3 dx ∧ dzi_v(α) ∧ β = (-23) ∧ (dx ∧ dy + 7 dz ∧ dx - 3 dy ∧ dz)= -23 dx ∧ dy - 161 dz ∧ dx + 69 dy ∧ dzα ∧ i_v(β) = (2 dx + 3 dy - 5 dz) ∧ (-3 dx ∧ dz)= 15 dy ∧ dx + 6 dz ∧ dx - 10 dy ∧ dz`

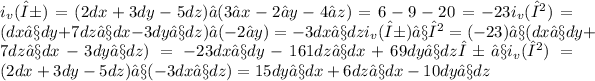
Therefore,
`i_v(α) ∧ β - α ∧ i_v(β) = (-23 dx ∧ dy - 161 dz ∧ dx + 69 dy ∧ dz) - (15 dy ∧ dx + 6 dz ∧ dx - 10 dy ∧ dz)= -23 dx ∧ dy - 171 dz ∧ dx + 79 dy ∧ dz`