Question

Find the maximum value of f(x, y) = x^3y^8 for x, y ≥ 0 on the unit circle. fmax= ____.

Answer 1

`f_(max)=(12288√(33))/(1771561) \approx 0.039846`

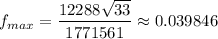
Explanation:

To find the maximum value of the function f(x, y) = x³y⁸ subject to the constraint that (x,y) lies on the unit circle, we can use Lagrange multipliers, a method that finds the local maxima and minima of a function subject to equality constraints.

`\hrulefill`

Step 1: Understanding the Constraint
`\hrulefill`

The unit circle constraint is x² + y² = 1. This equation defines the set of all points (x,y) whose distance from the origin is exactly 1. Since we are only interested in x,y≥0, we are effectively looking at the first quadrant of the unit circle.

`\hrulefill`

Step 2: Set up the Lagrange Multipliers
`\hrulefill`

The method of Lagrange multipliers states that at the maximum and minimum points, the gradient of our function f(x,y) will be proportional to the gradient of the constraint function g(x,y). Mathematically, this gives us the following system of equations:

`\\abla f(x,y)=\lambda \\abla g(x,y) \text{ with } g(x,y)=c`

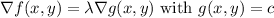
Let's calculate the gradient of f(x,y) and g(x,y) and set up the equations we need to solve:

For f(x,y):

`\Longrightarrow \\abla f(x,y)=\Big < (\partial f(x,y))/(\partial x) ,(\partial f(x,y))/(\partial y)\Big > \\\\\\\\\Longrightarrow \\abla f(x,y)=\Big < 3x^2y^8, \ 8x^3y^7 \Big >`

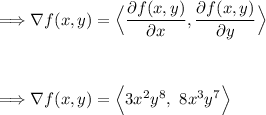
For g(x,y):

`\Longrightarrow \\abla g(x,y)=\Big < (\partial g(x,y))/(\partial x) ,(\partial g(x,y))/(\partial y)\Big > \\\\\\\\\Longrightarrow \\abla f(x,y)=\Big < 2x, \ 2y \Big >`

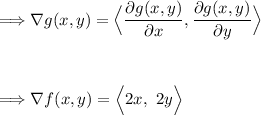
Now setting up our system of equations, we get:

`\left\{\begin{array}{ccc}3x^2y^8=2x\lambda& \dots (1)\\8x^3y^7=2y\lambda&\dots (2)\\x^2+y^2=1&\dots (3)\end{array}\right`

`\hrulefill`

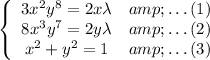
Step 3: Solve the System of Equations
`\hrulefill`

Taking equation (1):

`\Longrightarrow3x^2y^8=2x \lambda\\\\\\\\\Longrightarrow3x^2y^8-2x \lambda=0\\\\\\\\\Longrightarrow x(3xy^8-2 \lambda)=0\\\\\\\\\therefore \boxed{x=0} \text{ or } 3xy^8-2 \lambda=0 \ \dots (4)`

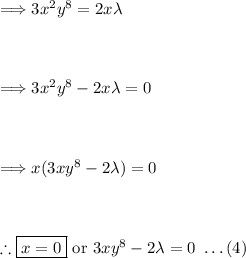
Taking equation (2):

`\Longrightarrow 8x^3y^7=2y\lambda\\\\\\\\\Longrightarrow 8x^3y^7-2y\lambda=0\\\\\\\\\Longrightarrow y(8x^3y^6-2\lambda)=0\\\\\\\\\therefore \boxed{y=0} \text{ or } 8x^3y^6-2\lambda \ \dots (5)`

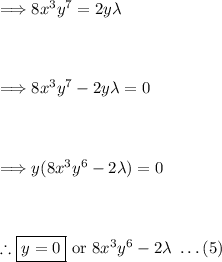
Taking equation (4):

`\Longrightarrow 3xy^8-2\lambda=0\\\\\\\\\Longrightarrow 2\lambda=3xy^8\\\\\\\\\therefore \lambda =(3)/(2) xy^8 \ \dots (6)`

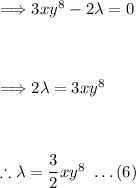
Taking equation (5):

`\Longrightarrow 8x^3y^6-2\lambda=0\\\\\\\\\Longrightarrow 2\lambda=8x^3y^6\\\\\\\\\therefore \lambda =4x^3y^6 \ \dots (7)`

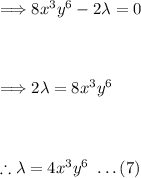
Take equation (6) and equation (7) and set them equal to eachother:

`\Longrightarrow(3)/(2)xy^8=4x^3y^6\\\\\\\\\Longrightarrow 3xy^8=8x^3y^6 \ \dots (8)`

Solve equation (8) for 'x':

`\Longrightarrow 3xy^8=8x^3y^6 \\\\\\\\\Longrightarrow 3y^8=8x^2y^6 \\\\\\\\\Longrightarrow x^2=(3)/(8)y^2\\\\\\\\\therefore x= \pm (y√(6))/(4) \ \dots (9)`

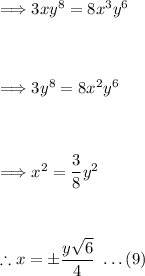
Solve equation (9) for 'y':

`\Longrightarrow x= \pm (y√(6))/(4) \\\\\\\\\therefore y=\pm (4x)/(√(6)) \ \dots (10)`

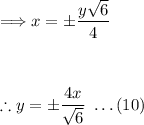
Substitute equation (9) into equation (3):

`\Longrightarrow \Big((y√(6))/(4)\Big)^2+y^2=1\\\\\\\\\Longrightarrow (3)/(8)y^2+y^2=1\\\\\\\\\Longrightarrow (11)/(8)y^2=1\\\\\\\\\therefore \boxed{y=\pm\sqrt{(8)/(11)} }`

`\hrulefill`

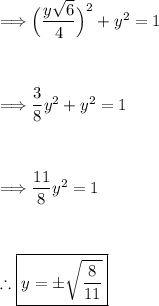
Step 4: Determine all of our Points
`\hrulefill`

Using equation (3) for the following calculations:

When x = 0:

`\Longrightarrow (0)^2+y^2=1\\\\\\\\\therefore \boxed{y=\pm1}`

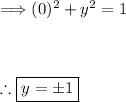
Thus, we have the points (0, 1) and (0, -1).

When y = 0:

`\Longrightarrow x^2+(0)^2=1\\\\\\\\\therefore \boxed{x=\pm1}`

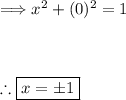
Thus, we have the points (1, 0) and (-1, 0).

When y = ±√(8/11):

`\Longrightarrow x^2+\Big(\pm\sqrt{(8)/(11)}\Big)^2=1\\\\\\\\ \Longrightarrow x^2=1-(8)/(11) \\\\\\\\\Longrightarrow x^2=(3)/(11)\\ \\\\\\\therefore \boxed{x=\pm \sqrt{(3)/(11)}}`

Thus, we have the points (-√(3/11), √(8/11)), (√(3/11), √(8/11)), (-√(3/11), -√(8/11)), and (√(3/11), -√(8/11)).

We have eight total points.

`\hrulefill`

Step 5: Finding the Maximum Value
`\hrulefill`

Plug in each point into the function f(x, y) = x³y to determine our maximum value.

`f(0,1)=f(0,-1)=f(1,0)=f(-1,0)=0\\\\\\\\f\Big(-\sqrt{(3)/(11)}, \sqrt{(8)/(11)}\Big)=f\Big(-\sqrt{(3)/(11)}, -\sqrt{(8)/(11)}\Big)=-(12288√(33))/(1771561) \ \therefore \text{Min. Value}\\\\\\\\f\Big(\sqrt{(3)/(11)}, \sqrt{(8)/(11)}\Big)=f\Big(\sqrt{(3)/(11)}, -\sqrt{(8)/(11)}\Big)=(12288√(33))/(1771561) \ \therefore \text{Max. Value}\\\\\\\\\therefore \boxed{\boxed{f_(max)=(12288√(33))/(1771561) \approx 0.039846}}`

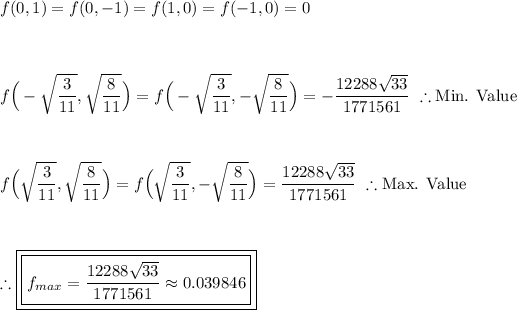
Thus, f_max is approximately 0.039846.

Answer 2

fmax = (12288√33)/1771561 ≈ 0.03984575513

Explanation:

You want the maximum value of the expression f(x, y) = x³y⁸ in the first quadrant of the unit circle.

Substitution

The unit circle has the equation ...

x² +y² = 1

This lets us write an expression for y²:

y² = 1 -x²

Using this in the definition of f(x, y), we can write ...

f(x) = x³(1 -x²)⁴

Maximum

The derivative of this function of x is ...

f'(x) = 3x²(1 -x²)⁴ +4x³(1 -x²)³(-2x) = (x²(1 -x²)³)·(3(1 -x²) -8x²)

This is zero at the critical points:

x = 0, x = 1, and 3 -11x² = 0, or x = √(3/11)

Then the maximum value of f is ...

f(√(3/11)) = (√(3/11))³(1 -3/11)⁴ = (√(3/11))(3/11)(8/11)⁴

fmax = 3·8⁴√33/11⁶

fmax = (12288√33)/1771561 ≈ 0.03984575513

__

Additional comment

The attached graph shows the curve f(x, y) and the unit circle constraint. The value of f(x, y) that makes the curves tangent is the one shown above.

<95141404393>