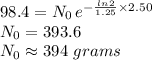Question

Potassium-40 decays into other elements wth a half half of 1.25 billion years. A geologist calculates a rock to be 2.50 billion years old. The rock contains 98.4 g of potassium-40. How much potassium-40 was initially in the rock?

Answer 1

394 grams initially in the rock

Half Life:

The activity of a radioactive isotope is measured by the isotope's half-life. Half-life is the time it takes for half of the nuclei in a radioactive sample to undergo radioactive decay. Radioisotopes can have half-lives from fractions of a second, to billions of years.

The formula for exponential decay, studied in mathematics, can be used to describe the amount of undecayed radioisotopes present after a certain amount of time:

`N_t = N_0\,e^{-\lambda t`

• Nt = amount of undecayed radioisotopes present after a time t
• N₀ = initial amount of radioisotopes

• λ = decay constant

When one half-life (denoted by
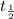`t_(1)/(2)` ) has elapsed, half the radioisotopes would have undergone radioactive decay. Hence after one half-life:

Nt = N₀/2, and we can write this equation as:

`(N_t)/(2) = N_0\,e^{-\lambda t_(1)/(2)`. Isolating λ to one side, we are left with the formula for the decay constant:

`\lambda = (ln2)/(t_(1)/(2) )`

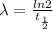
• λ = decay constant
• 
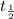  `t_(1)/(2)` = half-life

Therefore, if potassium-40 decays with a half-life of 1.25 billion:

• Nt = 98.4 g

• t = 2.50
• 
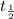  `t_(1)/(2)` = 1.25

We can calculate decay constant:

`\lambda = (ln2)/(t_(1)/(2) )\\\lambda = (ln2)/(1.25 )\\\\\lambda \approx 0.5545`

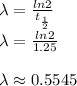
Hence:

`98.4= N_0\,e^{-(ln2)/(1.25)*2.50 }\\N_0 = 393.6\\N_0 \approx 394 \,\,grams`