Question

How many​ flowers, spaced every 3 ​in., are needed to surround a circular garden with a ​175-ft ​radius? Use 3.14 for pi.

Answer 1

First, we need to calculate the circumference of the circle. The formula for the circumference of the circle is:

`\text{C}=2\pi \text{r}`

If we substitute 175 ft for
`\text{r}` and use 3.14 to approximate
`\pi` we get a circumference of:

`\text{C}=2*3.14*175 \ \text{ft}`

`\text{C}=6.28*175 \ \text{ft}`

`\text{C}=1099 \ \text{ft}`

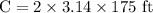
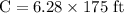
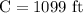
We can now convert the circumference in feet to inches:

`1099 \ \text{ft}* \frac{12 \ \text{in}}{1 \ \text{ft}} \implies`

`1099*12 \ \text{in}\implies`

`=13188`

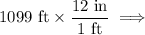
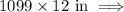
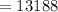
To find how many flowers we need we can divide the circumference in inches by the 3 inches between flowers giving:

`13188 \ \text{in}*\frac{1 \ \text{flower}}{3 \ \text{in}}\implies`

`13188 \ \text{in}*\frac{1 \ \text{flower}}{3 }\implies`

`\frac{13188 \ \text{flower}}{3 }\implies`

`=4396 \ \text{flower}`

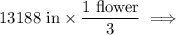
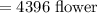
You would require 4,396 flowers