Question

Consider the integral given below

Answer 1

C ∫[-a,0] = -∫[0, a]

Explanation:

You want an alternate representation of the given integral ...

∫(2x⁵ -5x³)dx

on the interval [-a, a].

Odd function

The function f(x) = 2x⁵ -5x³ being integrated is an odd function. This means ...

f(-x) = -f(x) and f(0) = 0

Even function

An even function is characterized by ...

f(-x) = f(x)

The integral F(x) of this odd function f(x) is an even function, so the parts either side of x=0 have the integrals ...

`\displaystyle \int_(-a)^0{(2x^5-5x^3)}\,dx=F(0)-F(-a)=F(0) -F(a)`

`\displaystyle \int_0^a{(2x^5-5x^3)}\,dx=F(a)-F(0)`

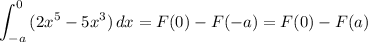
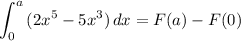
As we can see, these integrals are the opposites of each other, matching answer choice C.

__

Additional comment

The second attachment shows a numerical value for a=2.