Question

NO LINKS!!! URGENT HELP PLEASE!!!

Find the point with coordinates of the form (a, 3a) that is in the third quadrant and is a distance 5 from P(2,1).

(x, y) = __________

Answer 1

(-8.89, -26.69)

Explanation:

To find the point with coordinates of the form (a, 3a) that is in the third quadrant and is a distance 5 from P(2,1), we can use the following steps:

• Since the point is in the third quadrant, both the x-coordinate and the y-coordinate must be negative. Therefore, we can write (a, 3a) as (-|a|, -3|a|).

• We know that the distance between P(2,1) and (-|a|, -3|a|) is 5. We can use the distance formula to set up an equation and solve for |a|:

`√((2 - (-|a|))^2 + (1 - (-3|a|))^2) = 5\\√((2 + |a|)^2 + (1 + 3|a|)^2) = 5`

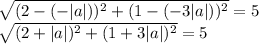
• Squaring both sides of the equation and simplifying, we get:

`a^2 + 8a - 8 = 0`

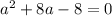
• Solving for a using the quadratic formula, we get:

`a = \frac{-8 ±√(8^2 - 4(1)(-8))} {(2(1))}\\a = (-8 ± √(96))/( 2)\\a = -4 ± 2√(6)`

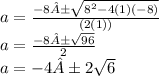
• Since the point is in the third quadrant, we want the negative root, so:

`a = -4 - 2\sqrt(6)`

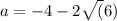
• Substituting this value of a into (-|a|, -3|a|), we get:

(x, y) =
`(-|-4 - 2\sqrt(6)|, -3|-4 - 2\sqrt(6)|)`

(x, y) ≈ (-8.89, -26.69)

Therefore, the point with coordinates of the form (a, 3a) that is in the third quadrant and is a distance 5 from P(2,1) is approximately (-8.89, -26.69).