Question

The equation -4x + y = 0 relates the

number of pages in a photo album y to
the number of pictures in the album x.
Tell whether the relationship is a direct
variation. Explain your answer.

Answer 1

Recall the general equation for a line in slope-intercept form:

`y=mx+b`

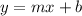
where:

`\text{y = y-coordinate}`

`\text{m}=\bold{slope}`

`\text{x = x-coordinate}`

`\text{b = y-intercept}`

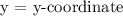
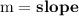
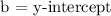
In this equation, if you isolate for
`y`, you end up with an equation that looks like this:

`-4x+y=0`

`-4x +4x+y=0+4x`

`\implies y=4x+0`

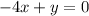
Recall that in direct variation, the graph goes through the origin, (0,0). Since the y-intercept of this equation is 0, this means the graph intersects the origin. Thus, this graph represents direct variation.

If you were to graph the line, you would see the intersection at (0,0):

graph
`\{y=4x [-12.66, 12.65, -6.33, 6.33]\}`