Question

HELP LOTS OF POINTS! You are on the ground looking at the top of a 1,000 foot tall building through binoculars at a 75 degree angle of elevation. Your eyes are 5 feet above the ground (consider this). How far away from the building are you standing? Round to the nearest tenth

Answer 1

266.6 ft

Explanation:

If a person stands at a point and looks up at an object, the angle between their horizontal line of sight and the object is called the angle of elevation.

To find how far away from the building you are standing, we need to find the distance labelled "x" on the attached diagram. We can do this by modelling the given scenario as a right triangle and solving for x by using the tangent trigonometric ratio.

Tangent trigonometric ratio

`\boxed{\tan \theta=\sf (O)/(A)}`

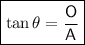
where:

• θ is the angle.
• O is the side opposite the angle.
• A is the side adjacent the angle.

Given information:

• Height of building = 1000 ft
• Person's eye level above the ground = 5 ft
• Angle of elevation = 75°

As your eyes are 5 ft above the ground, we have to model the line of sight as 5 ft above ground level. Therefore, the side of the right triangle opposite the angle of elevation is the height of the building less 5 ft:

`\implies \sf 1000 \; ft - 5\; ft=995 \; ft`

Let "x" be the horizontal distance between you and the building.

Therefore, the values to substitute into the tangent ratio are:

• θ = 75°
• O = 995
• A = x

Substitute these values into the ratio and solve for x:

`\tan 75^(\circ)=(995)/(x)`

`x=(995)/(\tan 75^(\circ))`

`x=266.609446...`

`x=266.6\; \sf ft\; (nearest\;tenth)`

Therefore, you are standing 266.6 ft from the building.