Question

The area of a rhombus is 20 square miles. One of its diagonals is 10 miles. What is the length of the missing diagonal?

Answer 1

The length of the missing diagonal is 4 miles.

Explanation:

To find the length of the missing diagonal, we can use the formula for the area of a rhombus, which is:

`\sf\qquad\dashrightarrow Area_((Rhombus)) = ((Diagonal_1 * Diagonal_2))/(2)`

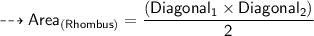
We know that the area is 20 square miles and one of the diagonals is 10 miles, so we can substitute these values into the formula as follows:

`\sf\qquad\dashrightarrow20 = ((10 * Diagonal_2))/(2)`

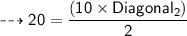
Simplifying the equation, we get:

`\sf\qquad\dashrightarrow 40 = 10 * Diagonal_2`

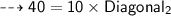
Dividing both sides by 10, we get:

`\sf\qquad\dashrightarrow \boxed{\bold{\:\:Diagonal_2 = 4\:\:}}\:\:\:\bigstar`

Therefore, the length of the missing diagonal is 4 miles.

Answer 2

The length of the missing diagonal is 4 miles.

Step-by-step explanation:

GIVEN :

• Area of rhombus = 20 square miles
• Diagonals of rhombus = 10 miles

TO FIND :

• Length of missing diagonals

USING FORMULA :

`\longrightarrow{\sf{Area \: of \: rhombus = (d_1 * d_2)/(3)}}`

SOLUTION :

Substituting the given values in the formula to find the length of the missing diagonal :

`\longrightarrow{\sf{Area \: of \: rhombus = (d_1 * d_2)/(3)}}`

`\longrightarrow{\sf{20 = (10 * d_2)/(2)}}`

`\longrightarrow{\sf{20 * 2= 10 * d_2}}`

`\longrightarrow{\sf{40= 10 * d_2}}`

`\longrightarrow{\sf{d_2 = (40)/(10)}}`

`\longrightarrow{\sf{d_2 = \cancel{(40)/(10)}}}`

`\longrightarrow{\sf{\underline{\underline{d_2 = 4 \: miles}}}}`

Hence, the length of the missing diagonal is 4 miles.