the true statements are:
- The minimum value of the function is 5.8.
- The amplitude of the function is 1.5.
The table provides the height of a windmill blade at various times, and we can use it to determine the characteristics of the sinusoidal function that models this motion. Here's the data from the table:
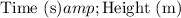
Now let's analyze each statement:
1. The frequency of the function is 4.
- Frequency refers to the number of cycles the function completes in a unit time interval. In this case, we see that the windmill blade goes from one peak to the next in a time span of 4 seconds (from 2 seconds to 6 seconds). This represents half a cycle, so in 4 seconds, the frequency is not 4; rather, it's \( \frac{1}{2} \) cycles per 4 seconds or \( \frac{1}{8} \) cycles per second.
2. The minimum value of the function is 5.8.
- The minimum height reached by the windmill blade, as shown in the table, is 5.8 meters. This statement is true.
3. The amplitude of the function is 1.5.
- The amplitude of a sinusoidal function is the distance from the middle value to the maximum or minimum value. The middle value of this function is the average of the minimum and maximum, which is
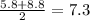meters. The maximum is 8.8 meters, so the amplitude is
meters. This statement is true.
4. The period of the function is 1/4.
- The period of a sinusoidal function is the time it takes to complete one full cycle. From the data, we can see that the function completes a full cycle every 4 seconds (from time 0 to time 4). Therefore, the period is 4 seconds, not
seconds.
Based on the data provided, the true statements are:
- The minimum value of the function is 5.8.
- The amplitude of the function is 1.5.