Question

The length of one leg of a right triangle is 2 times the length of the other, and the

length of the hypotenuse is 12. What is the length of the longest leg?

Answer 1

`(24√(5) )/(5)`

Explanation:

Let's start by assigning one of the unknown legs with the variable x.

We know that the other leg is 2 times the length of x, so we can write:

2x

We also know that the length of the hypotenuse is 12.

From here, we can use the Pythagorean Theorem.

Recall that the Pythagorean Theorem is:

`a^2+b^2=c^2`

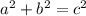
where a is the length of one leg, b is the length of the other leg, and c is the length of the hypotenuse.

Let's substitute the values. We have:

`x^2+(2x^2)=12^2=\\x^2+4x^2=144=\\5x^2=144=\\x^2=(144)/(5)=\\x=(12)/(√(5) )`

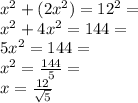
Let's rationalize the denominator by multiplying the numerator and denominator by
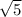`√(5)`, like so:

`(12)/(√(5) ) =\\(12√(5) )/(5)`

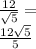
Therefore,
`x=(12√(5) )/(5)`

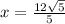
Let's solve for 2x:

`2x=\\2((12√(5) )/(5))=\\ (24√(5) )/(5)`

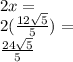
So, the length of the longest leg is
`(24√(5) )/(5)`