Question

John puts $70 in a savings account that earns 6% annually. The interest is not compounded. How many years will it take John to make at least $100 in interest?

Answer 1

approx. 24 years

Explanation:

The formula to find the simple interest is:

`\sf I= (prt)/(100)`

Here,

I ⇒ Interest ⇒ $ 100

p ⇒ principle ⇒ $ 70

r ⇒ rate ⇒ 6

t ⇒ time ( years )

Let us find the time taken using the formula.

`\sf I= (prt)/(100)\\\\100=(70*6*t)/(100) \\\\100*100=420t\\\\10000=420t\\\\23.8\: years=t\\\\approx. \:24 \:years=t`

Answer 2

24 years

Explanation:

If interest is not compounded, it is called simple interest.

Simple interest is calculated as a percentage of the principal amount and is applied only to the principal.

The formula for simple interest is:

`\boxed{\sf I = Prt}`

where:

• I = Total interest earned.
• P = Principal amount.
• r = Interest rate (in decimal form).
• t = Time (in years).

The given values are:

• I = $100
• P = $70
• r = 6% = 0.06

Substitute the given values into the formula and solve for t:

`\implies \sf 100=70 \cdot 0.06 \cdot t`

`\implies \sf 100=4.2 t`

`\implies \sf 4.2 t=100`

`\implies \sf (4.2 t)/(4.2)=(100)/(4.2)`

`\implies \sf t=23.8095238...\;years`

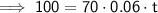
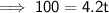
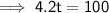
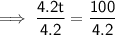
We need to round up to the next year. Therefore, it will take 24 years for John to make at least $100 in interest.