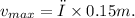Final Answer:
The maximum speed of a point on the outside of the wheel, located 15 cm from the axle, can be determined using the formula
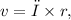 where \
where \
 is the linear velocity,
is the linear velocity,
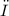 is the angular velocity, and
is the angular velocity, and
 is the radial distance from the axle. Assuming a constant angular velocity, the maximum linear speed can be calculated as
is the radial distance from the axle. Assuming a constant angular velocity, the maximum linear speed can be calculated as
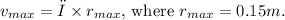
Step-by-step explanation:
The linear velocity
 of a point on a rotating object is given by the product of its angular velocity
of a point on a rotating object is given by the product of its angular velocity
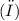 and the radial distance
and the radial distance
 from the axis of rotation. In this case, the maximum speed occurs at the outer edge of the wheel, which is 15 cm or 0.15 meters from the axle. The formula for linear velocity is
from the axis of rotation. In this case, the maximum speed occurs at the outer edge of the wheel, which is 15 cm or 0.15 meters from the axle. The formula for linear velocity is
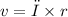 . To find the maximum speed
. To find the maximum speed
 we use the maximum radial distance,
we use the maximum radial distance,
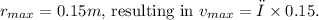
Angular velocity
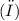 is the rate at which the object rotates. If not provided, it can be determined using the formula
is the rate at which the object rotates. If not provided, it can be determined using the formula
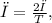 where
where
 is the period of one complete revolution. However, if the angular velocity is given, it can be directly substituted into the formula. Once
is the period of one complete revolution. However, if the angular velocity is given, it can be directly substituted into the formula. Once
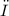 is determined, it is multiplied by the maximum radial distance
is determined, it is multiplied by the maximum radial distance
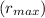 to find the maximum linear speed
to find the maximum linear speed
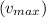 . Thus, the maximum speed of a point on the outside of the wheel, 15 cm from the axle, is
. Thus, the maximum speed of a point on the outside of the wheel, 15 cm from the axle, is