Answer:
Step-by-step explanation:
1.
From the given information;
The spot rate for maturity at 0.5 year
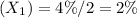
The spot rate for maturity at 1 year is:
=
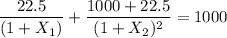
=
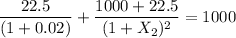
=
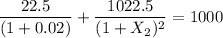
By solving for
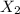 ;
;
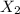 = 2.253%
= 2.253%
The spot rate for maturity at 1.5 years is:
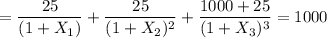
Solving for
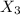
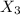 = 2.510%
= 2.510%
The spot rate for maturity at 2 years is:
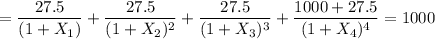
By solving for
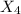 ;
;
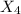 = 2.770%
= 2.770%
Recall that:
Coupon rate = yield to maturity for par bond.
Thus, the annual coupon rates are 4%, 4.5%, 5%, and 5.5% for 0.5, 1, 1.5, 2 years respectively.
2.
For n years, the price of n-bond is:
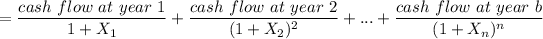
Thus, for 2 years bond implies 4 periods;
∴
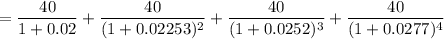
= $1047.024
3.
Suppose there exist no-arbitrage, then the price is:
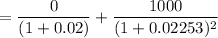
= 956.4183
Since the market price < arbitrage price.
We then consider 0.5, 1-year bonds from the portfolio
Now;
weight 2 × 1000 + weight 2 × 22.5 = 1000
weight 2 × 1022.5 = 1000
weight 2 = 1022.5/1000
weight 2 = 0.976
weight 1 + weight 2 = 1
weight 1 = 1 - weight 2
weight 1 = 1 - 0.976
weight 1 = 0.022
The price of a 0.5-year bond will be:
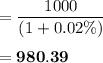
The price of a 1-year bond will be = 1000
Market value on the bond portfolio = 0.022 × price of 0.5 bond + 0.978 × price 1-year bond = 956.42
= 0.022 × 980.39 + 0.978 × 1000
= 956.42
So, to have arbitrage profit, the investor needs to purchase 1 unit of the 1-year zero-coupon bond as well as 0.022 units of the 0.5-year bond. Then sell 0.978 unit of the 1-year bond.
Then will he be able to have an arbitrage profit of $56.42
4.
The one-period ahead forward rates can be computed as follows:
Foward rate from 0 to 0.5
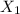 = 2%
= 2%
Foward rate from 0.5 to 1
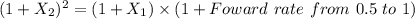
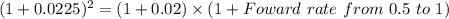
Foward rate from 0.5 to 1 = 2.5%
Foward rate from 1 to 1.5
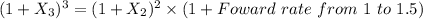
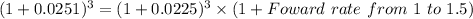
Foward rate from 1 to 1.5 =3.021%
Foward rate from 1.5 to 2
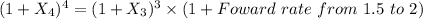
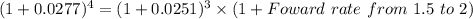
Foward rate from 1.5 to 2 =3.021%
5.
The expected price of the bond if the hypothesis hold :
=
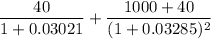
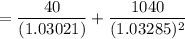
= 1013.724254
= 1013.72