Question

If a light ray travels from air into glass that has a refractive index of 1.6, and the incident light ray makes an angle with the normal that's 31 degrees, what angle will the transmitted ray make with the normal? Enter your answer using two significant figures. Enter the number only, not the units, which should be degrees. 19 Question 2 Incident Ray Normal Medium 1 Medium 2 Refracted Ray 1 pts What angle will the reflected light ray make relative to the normal, in the previous problem? Enter your answer using two significant figures. Enter the number only, not the units, which should be degrees.​

Answer 1

Using Snell's law, we can find the angle the transmitted ray will make with the normal:

`n1sin(theta1) = n2sin(theta2)`

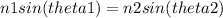
Where
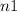`n1` is the refractive index of the incident medium (air),
`theta1` is the angle the incident ray makes with the normal,
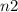`n2` is the refractive index of the second medium (glass), and
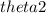`theta2` is the angle the transmitted ray makes with the normal.

Plugging in the given values, we get:

`(1.00)(sin(31)) = (1.6)(sin(theta2))`

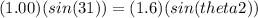
Solving for
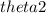`theta2`, we get:

`theta2 = sin^(-1)((1.00)*(sin(31))/(1.6)) = 19 degrees (rounded to two significant figures)`

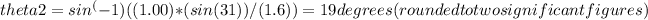
To find the angle the reflected ray makes with the normal, we can use the fact that the angle of incidence is equal to the angle of reflection:

`theta1 = theta_r`

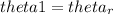
where
`theta_r` is the angle the reflected ray makes with the normal.

Plugging in the given value of
`theta1`, we get:

`theta_r` = 31 degrees