Question

Please help someone..50 points​

Answer 1

We can find the sum of the interior angles of any polygon using the formula

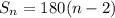`S_(n)=180(n-2)`, where n is the number of sides.

Because each of these polygons have four sides, we can use one formula where our n is 4 to find the sum of the interior angles:

`S_(4)=180(4-2)\\ S_(4)=180*2\\ S_(4)=360`

Thus, for all four problems, we can set the four angles equal in the four polygons equal to 360 and solve for the variables

(15) *Note the right angle symbol in this problem which always equals 90°

`84+90+(2x+118)+(2x+68)=360\\174+2x+118+2x+68=360\\360+4x=360\\4x=0\\x=0`

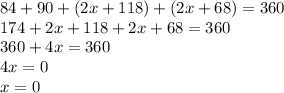
Now, to find the measure of <Y, we simply plug in 0 for x in its equation

m<Y = 2(0) + 118 = 118°

(16):

`82+105+(8x+11)+10x=360\\187+8x+11+10x=360\\198+18x=360\\18x=162\\x=9`

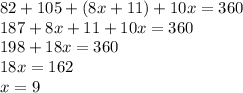
To find the measure of <F, we plug in 9 for x in its equation

m<F = 10(9) = 90°

(17):

`95+95+(10x-5)+(8x+13)=360\\190+10x-5+8x+13=360\\198+18x=360\\18x=162\\x=9`

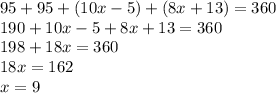
To find the measure of <M, we plug in 9 for x in its equation

m<M = 10(9) - 5 = 85°

(18):

`(14x-7)+(11x-2)+93+76=360\\14x-7+11x-2+169=360\\25x+160=360\\25x=200\\x=8`

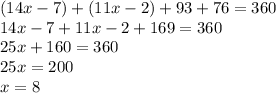
To find the measure of <M, we plug in 8 for x in its equation

m<M = 11(8) - 2 = 86°