Answer:
The answer would be absolute value. At absolute zero temperature (0 K°), all forces in the universe are gone: strong force, weak force, electromagnetic force, gravity force, there is no movement, no structure… it is unimaginable, utterly horrible.
Step-by-step explanation:
One thing is: Don’t worry, that will never happen.
This universe is spontaneously, simultaneously thermodynamically balanced in natural thermodynamic entropy mutual transformation cycles (Q↓→E↑) ↔ (E↓→ Q↑) in their corresponding order conversion efficiency of (ɳ=E/Q) ↔ (1/ɳ=Q/E), ∑ ∆(mc² + mv) = ∑ ∆(mx + mc), (16), in the black hole --- galaxy complex: ∑ (mc² + mv) ↔ ∑ (mx + mc), (17). In quantum level thermodynamic entropy transformation unit of the black hole --- galaxy complex as the only concentrative – dissipative structure in the universe, it will keep the basic thermodynamic entropy mutual transformation unit thermodynamically balanced, and thermodynamic balance will keep all other balances. And due to these basic thermodynamic units composed of the universe, the whole universe is balanced in every way.
This world had been like this from startles past and will be like this to endless future.
Natural process spontaneously keeps thermodynamic existence balanced continuation but to do so, it spontaneously cuts off the information existence evolutionary continuation to allow that to happen.
Though the nature does give intelligent lives a way out to allow the rare rationally rational being to use their rationality ability to form a rational open process to connect the limited natural processes to reach the endless future. Due to this rational life is a tiny proportion of the mass of the universe, and they are so much rational, they will never disturb the thermodynamic balance of this universe --- they coexist with this universe as eternal life, they are the real meaning of this universe --- the effective information E.
You may wonder, can the temperature ever drop below absolute zero?
Negative absolute temperature is indeed possible. In fact, researchers achieved this in 2013.
Here’s the thing though: Negative absolute temperature isn’t colder than absolute zero; it’s actually hotter than infinity (that’s messed up, right?).
Achieving this depends on the use of the general thermodynamic definition of temperature, rather than the “kinetic” definition that everyone learns in high school (i.e. that temperature is a measure of the average kinetic energy of the molecules in a system).
Turns out that the kinetic definition isn’t entirely general. So, instead, thermodynamics defines temperature using:
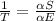
Or, in words:
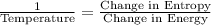
So how do you get negative temperature from that?
Well, the way that a system normally appears in nature is that its molecules have high probability of being found in low energy states, and a low probability of being in high energy states. This is true even for things that are conventionally very hot.
When we add energy to such a system, we promote some of its molecules to higher energy states. Since entropy is proportional to the natural log of the number of microstates of the system, it follows that the entropy of the system increases as its molecules attain higher energy (the number of possible arrangements, or microstates, of the system increases).
So entropy increases with energy. That makes
 positive and so T is positive.
positive and so T is positive.
Suppose, though, that you find a way to invert that system, so that its molecules have high probability of being found in high energy states, and low probability of being found in low energy states. And, suppose, further, that the molecules of that system have an upper bound on the energy they can absorb.
Adding energy to the inverted system, then, causes it to tend toward a state where all the molecules have their energy maximized. As there are only a small number of ways to arrange such system, the system’s entropy will tend toward zero as energy increases. And that means that entropy is decreasing.
So, in the inverted system, entropy decreases with increasing energy. That makes
 negative, and so T
negative, and so T
is negative. We’ve achieved negative temperature!
In between the increasing entropy state and the decreasing entropy state, there will be a maximum entropy state. If you’ve taken first year calculus, you’ll remember that, as we approach that maximum,
 approaches zero. This means that T
approaches zero. This means that T
must be approaching infinity.
Positive temperatures occur to the left of the peak, and negative temperatures to the right of the peak. The insets show the distribution of molecular energies at the corresponding temperatures.
Note that the contrived negative temperature system we’re discussing here cannot be measured conventionally, by putting a thermometer into equilibrium with the system.