Answer:
Domain:
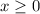
Range:

Explanation:
Recall that the domain of a function is the values that x can be, while the range of a function is the values that y can be.
Let's take a look at one part of the function:
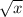 .
.
The square root of any positive number does exist. It may not be rational, but it exists. The square root of zero also exists -- it's zero.
However, the square root of a negative number will never exist - it's imaginary. So, x cannot be negative as long as it is under the radical.
The domain is:
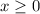
Now, to find the range, let's look at the coefficient: -3.
A negative number times a negative number is positive. A negative number times a positive number is negative.
However, x can never be negative, so no matter what real value you plug in for x, you will always be multiplying -3 by a positive number (or zero).
Since zero times any number is zero, and a positive number times a negative number is a negative number, y will always be either equal to zero or negative.
So, the range is:
