Question

A company is developing its weekly production plan. The company produces two products, A and B, which are processed in two departments. Setting up each batch of A requires $60 of labor while setting up a batch of B costs $80. Each unit of A generates a profit of $17 while a unit of B earns a profit of $21. The company can sell all the units it produces. The data for the problem are summarized below.

Hours required by
Operation A B Hours
Cutting 3 4 48
Welding 2 1 36
The decision variables are defined as:
xi = the amount of product i produced
yi = 1 if xi > 0 and 0 if xi = 0
A spreadsheet implementation of the problem is shown below.
Q1. What is the objective function for this problem?
a. Maximize: 17x1 + 21x2 - 60y1 - 80y2
b. Minimize: 60y1 + 80y2
c. Minimize: 17x1 + 21x2 - 60y1 - 80y2
d. d. Maximize: 17x1 + 21x2
Q2. What is the appropriate formula to use in cell E8 of the Excel implementation of the ILP model for this problem?
a. =SUMPRODUCT(B8:C8,B14:C14) - SUMPRODUCT(B5:C5,B7:C7)
b. =SUMPRODUCT(B5:C5,B7:C7) - SUMPRODUCT(B8:C8,B14:C14)
c. =SUMPRODUCT(B5:C5,B7:C7) - SUMPRODUCT(B8:C8,B15:C15)
d. =SUMPRODUCT(B5:C5,B7:C7) - B8:C8
Q3. Which of the following algebraic constraints creates the link between setting up to produce A's and making some A's for this problem?
a. x1 - 18 y1 > 0
b. x1 - y1 = 0
c. = if(x1 > 0, y1 = 1, y1 = 0)
d. x1 < 16y1

Answer 1

The responses to this question can be defined as follows:

Step-by-step explanation:

In question 1, the objective function to solve the given problem is:
`\text{Maximize:} 17x_1 + 21x_2 - 60y_1 - 80y_2`

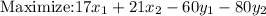
In question 2, "
`=\text{SUMPRODUCT}(B5:C5,B7:C7) - \text{SUMPRODUCT}(B8:C8,B14:C14)` "

is the appropriate choice for the formula, which is using in cell E8, and it is also used in the ILP model.

In question 3, the choice "
`x_1 < 16y_1`" is used in the algebraic constraint for creating the link between setting up to produce A's and making some A's.