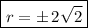Question

R^{2} =8 solving equations using square roots

Answer 1

`r=\pm\,2\sqrt2`

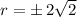
Explanation:

Given the equation:

`r^2=8`,

we can solve for
`r` by taking the square root of both sides.

`√(r^2)=\pm√(8)`

But, we must remember the even root property, which states that if
`x^2 = a`, where
`a` is a non-negative real number, then
`x = \pm \sqrt a`, because both
`(-a)^2` and
`a^2` result in
`a`.

______________

For example, if you want to find the square root of 25, you know that 5 × 5 = 25, so
`√(25)` = 5. However, (-5) × (-5) also equals 25, so (-5) is also a valid solution for
`√(25)`.

‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾

`r=\pm√(8)`

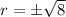
Now, we can simplify the square root by prime factoring it.

`r=\pm√(2 \cdot 2\cdot2)`

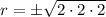
We can see that there is one complete pair of 2's, so we can take those out of the square root.

`\boxed{r=\pm\, 2\sqrt2}`