Question

Find the 25th term.
2, 10, 18, 26, 34, ...
25th term = [?]

Answer 1

an = a1 + (n - 1)d

Substituting the values

an = 2 + (n - 1)8

We have to find the 25th term n = 25

a25 = 2 + (25 - 1)8

a25 = 2 + (24)8

a25 = 2 + 192

a25 = 194

Answer 2

Answer: 194

======================================================

Step-by-step explanation:

The gap between adjacent terms is 8.

• 2+8 = 10
• 10+8 = 18
• 18+8 = 26
• 26+8 = 34
• etc

The long way to get the answer would be to keep adding 8 to each term to generate the next one. You'd need to do this 20 times. There are 5 terms here already, so you need 25-5 = 20 more operations of "add 8".

I don't recommend this option. I recommend the shortcut mentioned in the next section.

--------

The shortcut would be to find the nth term of the arithmetic sequence

`a_1 = 2 = \text{ first term}\\\\d = 8 = \text{ common difference}\\\\a_n = \text{ nth term}\\\\a_n = a_1 + d(n-1)\\\\a_n = 2 + 8(n-1)\\\\`

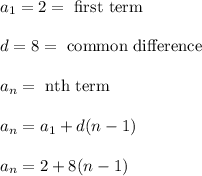
As a check, plug n = 1 into that formula to get
`a_1 = 2`. Plug n = 2 to get
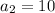`a_2 = 10` and so on. I'll leave this check portion for the student to do.

--------

The last step is to plug n = 25 into that formula to determine the 25th term.

`a_n = 2 + 8(n-1)\\\\a_(25) = 2 + 8(25-1)\\\\a_(25) = 2 + 8(24)\\\\a_(25) = 2 + 192\\\\a_(25) = 194\\\\`

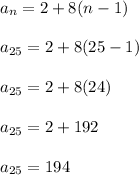
The final answer is 194

-------

Extra section (optional):

We can use a spreadsheet to generate the 25 terms. This is to help check the answer.

2, 10, 18, 26, 34, 42, 50, 58, 66, 74, 82, 90, 98, 106, 114, 122, 130, 138, 146, 154, 162, 170, 178, 186, 194