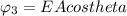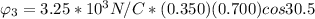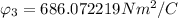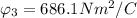Question

An electric field of intensity 3.25 kN/C is applied along the x-axis. Calculate the electric flux through a rectangular plane 0.350 m wide and 0.700 m long if the following conditions are true. (a) The plane is parallel to the yz-plane. N · m2/C (b) The plane is parallel to the xy-plane. N · m2/C (c) The plane contains the y-axis, and its normal makes an angle of 30.5° with the x-axis. N · m2/C

Answer 1

`\varphi_1= 796.25 N m^2/C`

`\varphi_2= 0 N m^2/C`

`\varphi_3=686.1 N m^2/C`

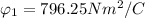
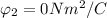
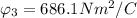
Step-by-step explanation:

From the question we are told that

Electric field of intensity
`E= 3.25 kN/C`

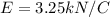
Rectangle parameter Width
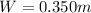`W=0.350 m` Length
`L=0.700 m`

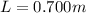
Angle to the normal
`\angle=30.5 \textdegree`

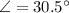
Generally the equation for Electric flux at parallel to the yz plane
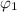`\varphi_1` is mathematically given by

`\varphi_1=EA cos theta`

`\varphi_1=3.25* 10^3 N/C * ( 0.350)(0.700) cos 0`

`\varphi_1= 796.25 N m^2/C`

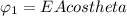
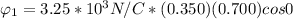
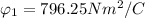
Generally the equation for Electric flux at parallel to xy plane
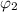`\varphi_2` is mathematically given by

`\varphi_2=EA cos theta`

`\varphi_2=3.25* 10^3 N/C * ( 0.350)(0.700) cos 90`

`\varphi_2= 0 N m^2/C`

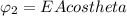
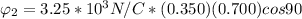
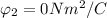
Generally the equation for Electric flux at angle 30 to x plane
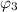`\varphi_3` is mathematically given by

`\varphi_3=EA cos theta`

`\varphi_3=3.25* 10^3 N/C * ( 0.350)(0.700) cos 30.5`

`\varphi_3=686.072219 N m^2/C`

`\varphi_3=686.1 N m^2/C`