Question

A student of mass M is standing on a scale plate placed on the floor of an elevator. When the elevator is not moving, the reading N on the scale is N = Mg. At some later time, the elevator is moving upward with speed v and slowing down with an acceleration of magnitude a. Based on these data, which of the following statements about N must be correct?answer choicesN=m(g+v)N=mgN=m(g-v)N=m(g+a)N=m(g-a)

Answer 1

The reading on the scale will be
`M\, (g - a)`.

Step-by-step explanation:

There are two forces on this student:

• Weight (downward, from the earth), and
• Normal force (upward, from the scale on the floor.)

If the gravitational field strength is
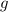`g`, the weight on the student would be
`M\, (-g)`.

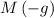The resultant net force on the student will be:

`(\text{net force}) = (\text{weight}) + (\text{normal force})`.

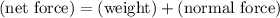At the same time, the resultant net force on the student is proportional to acceleration:

`(\text{net force}) = (\text{mass})\, (\text{acceleration})`.

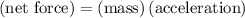When the elevator is not moving, acceleration of the student will be
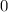`0`. Therefore:

`(\text{net force}) = (\text{mass})\, (\text{acceleration}) = (M)\, (0) = 0`.

`(\text{weight}) + (\text{normal force}) = (\text{net force}) = 0`.

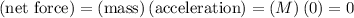Also note that
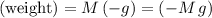`(\text{weight}) = M\, (-g) = (-M\, g)` regardless of the motion of the student. Rearrange the equation to find
`(\text{normal force})`:

`\begin{aligned} (\text{normal force}) &= (\text{net force}) - (\text{weight}) \\ &= 0 - (-M\, g) \\ &= M\, g\end{aligned}`.

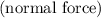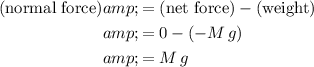Note that this value is the same as the reading on the scale. Thus, the question implies that the scale in this question is measuring the normal force on the student (instead of the mass of the student.)

Assume that the student is slowing down. Since acceleration measures the rate of change in velocity, the acceleration of the student will be negative since velocity is decreasing. Hence, the acceleration of the student would be
`(-a)`.

`(\text{net force}) = (\text{mass})\, (\text{acceleration}) = M\, (-a)`.

`\begin{aligned} (\text{normal force}) &= (\text{net force}) - (\text{weight}) \\ &= M\, (-a) - (-M\, g) \\ &= M\, (g - a)\end{aligned}`.

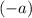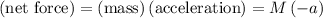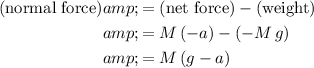Hence, the reading on this scale would be
`M\, (g - a)`.