Answer:
The reading on the scale will be
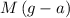 .
.
Step-by-step explanation:
There are two forces on this student:
- Weight (downward, from the earth), and
- Normal force (upward, from the scale on the floor.)
If the gravitational field strength is
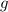 , the weight on the student would be
, the weight on the student would be
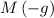 .
.
The resultant net force on the student will be:
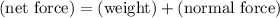 .
.
At the same time, the resultant net force on the student is proportional to acceleration:
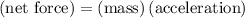 .
.
When the elevator is not moving, acceleration of the student will be
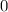 . Therefore:
. Therefore:
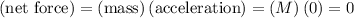 .
.
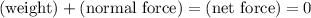 .
.
Also note that
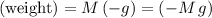 regardless of the motion of the student. Rearrange the equation to find
regardless of the motion of the student. Rearrange the equation to find
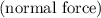 :
:
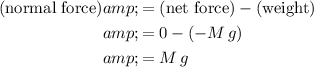 .
.
Note that this value is the same as the reading on the scale. Thus, the question implies that the scale in this question is measuring the normal force on the student (instead of the mass of the student.)
Assume that the student is slowing down. Since acceleration measures the rate of change in velocity, the acceleration of the student will be negative since velocity is decreasing. Hence, the acceleration of the student would be
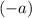 .
.
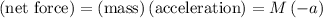 .
.
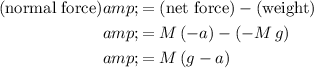 .
.
Hence, the reading on this scale would be
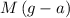 .
.