Question

If $20,000 is invested at an interest rate of 2% per year, compounded semiannually, find the value of the investment after the given number of years. (Round your answers to the nearest cent.)

6 years
12 years
18 years

Answer 1

6 years = $22,536.50

12 years = $25,394.69

18 years = $28,615.38

Explanation:

The find the value of the investment after the given number of years, first create an equation for A in terms of t using the compound interest formula.

Compound Interest Formula

`\boxed{\sf A=P\left(1+(r)/(n)\right)^(nt)}`

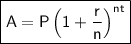
where:

• A = Final amount.
• P = Principal investment.
• r = Interest rate (in decimal form).
• n = Number of times interest is applied per year.
• t = Time (in years).

Given values:

• P = $20,000
• r = 2% = 0.02
• n = 2 (semi-annually)

Substitute the given values into the formula to create an equation for the value of the investment, A, in terms of time in years, t:

`\implies \sf A=20000\left(1+(0.02)/(2)\right)^(2t)`

`\implies \sf A=20000\left(1+0.01\right)^(2t)`

`\implies \sf A=20000\left(1.01\right)^(2t)`

`\hrulefill`

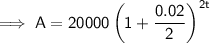
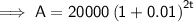
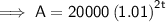
To find the value of the investment after 6 years, substitute t = 6 into the equation:

`\implies \sf A=20000\left(1.01\right)^(2\cdot 6)`

`\implies \sf A=20000\left(1.01\right)^(12)`

`\implies \sf A=20000(1.12682503...)`

`\implies \sf A=22536.5006026...`

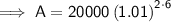
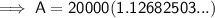
Therefore, the value of the investment after 6 years is $22,536.50 rounded to the nearest cent.

`\hrulefill`

To find the value of the investment after 12 years, substitute t = 12 into the equation:

`\implies \sf A=20000\left(1.01\right)^(2 \cdot 12)`

`\implies \sf A=20000\left(1.01\right)^(24)`

`\implies \sf A=20000\left(1.2697346...\right)`

`\implies \sf A=25394.69297...`

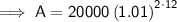
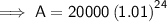
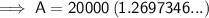
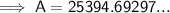
Therefore, the value of the investment after 12 years is $25,394.69 rounded to the nearest cent.

`\hrulefill`

To find the value of the investment after 18 years, substitute t = 18 into the equation:

`\implies \sf A=20000\left(1.01\right)^(2\cdot 18)`

`\implies \sf A=20000\left(1.01\right)^(36)`

`\implies \sf A=20000\left(1.43076878...\right)`

`\implies \sf A=28615.37567...`

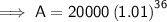
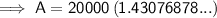
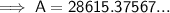
Therefore, the value of the investment after 18 years is $28,615.38 rounded to the nearest cent.