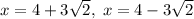Question

50 POINTS!!!! Rewrite the function by completing the square f(x) = x^2 - 8x - 2

Answer 1

The rewritten function by completing the square is:

`f(x)=(x-4)^2-18`

The solutions of the function are:

`x=4+3√(2),\;x=4-3√(2)`

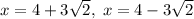
Explanation:

Given function:

`f(x)=x^2-8x-2`

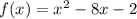
To rewrite the function by completing the square, begin by adding and subtracting the square of half the coefficient of the term in x. (Place these between the term in x and the constant).

`f(x)=x^2-8x+\left((-8)/(2)\right)^2-\left((-8)/(2)\right)^2-2`

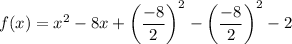
Simplify:

`f(x)=x^2-8x+\left(-4\right)^2-\left(-4\right)^2-2`

`f(x)=x^2-8x+16-16-2`

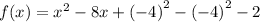
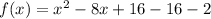
We have now created a perfect square trinomial from the first three terms: x² - 8x + 16.

`\boxed{\begin{minipage}{8.5 cm}\underline{\sf \large Perfect Square Trinomial}\\\\\sf A perfect square trinomial is a polynomial of the form $a^2 + 2ab + b^2$ or $a^2 - 2ab + b^2$, where $a$ and $b$ are constants. \\\\When factored, a perfect square trinomial becomes the square of a binomial: $(a + b)^2$ or $(a - b)^2$. \\\end{minipage}}`

Factor the perfect square trinomial x² - 8x + 16.

`f(x)=(x-4)^2-16-2`

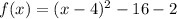
Simplify by subtracting the numbers outside the parentheses:

`f(x)=(x-4)^2-18`

Therefore, the given function rewritten by completing the square is:

• f(x) = (x - 4)² - 18

The solutions to a quadratic function are the x-values which satisfy the equation f(x) = 0. Therefore, to find the solutions, set the function equal to zero and solve for x.

`\begin{aligned}f(x)&=0\\\implies (x-4)^2-18&=0\\(x-4)^2-18+18&=0+18\\(x-4)^2&=18\\√((x-4)^2)&=√(18)\\x-4&=\pm√(18)\\x-4+4&=\pm√(18)+4\\x&=4\pm√(18)\\x&=4\pm√(3^2 \cdot 2)\\x&=4\pm√(3^2) √(2)\\x&=4\pm3 √(2)\end{aligned}`

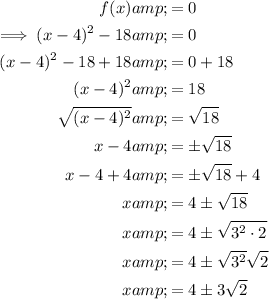
Therefore, the solutions of the function are:

`x=4+3√(2),\;x=4-3√(2)`